Untuk menemukan akar-akar persamaan kuadrat dengan cara melengkapkan kuadrat sempurna, syarat pertama adalah koefisien 𝑥² yaitu a harus sama dengan 1 agar mudah difaktorkan. Jika a bukan 1, bagilah persamaan oleh koefisien 𝑥² sehingga diperoleh a sama dengan 1.
Jika di ruas kiri persamaan sudah muncul suku
𝑥² + 2(b/2)𝑥 + (b/2)²
maka faktorkan menjadi (𝑥 + b/2)² . Yang mana pemfaktoran ini syah karena
𝑥² + 2(b/2)𝑥 + (b/2)² = (𝑥 + b/2)²
Selanjutnya langkah-langkah melengkapkan kuadrat sempurna adalah sebagai berikut:
-Pada persamaan kuadrat
𝑥² + b𝑥 + c = 0
kurangi ruas kiri dan ruas kanan oleh c (jika c < 0, ini akan menjadi penambahan)
𝑥² + b𝑥 + c - c= 0 - c
⇒𝑥² + b𝑥 = - c
-Tambahkan suku (b/2)² pada ruas kiri dan ruas kanan
𝑥² + b𝑥 + (b/2)² = (b/2)² - c
-Modifikasi suku b𝑥 menjadi 2(b/2)𝑥
𝑥² + 2(b/2)𝑥 + (b/2)² = (b/2)² - c
-Ubah ruas kiri persamaan menjadi
(𝑥 + b/2)² = (b/2)² - c
-Ambil akar dari ruas kiri dan kanan
-Kurangkan ruas kiri dan ruas kanan oleh b/2 (jika b < 0, ini akan menjadi penambahan)
Tanda ± artinya rumus menangani dua operasi yaitu penjumlahan dan pengurangan.
-Akar 𝑥₁ diperoleh dengan mengambil tanda +
-Akar 𝑥₂ diperoleh dengan mengambil tanda -
Contoh 1. tentukan akar-akar persamaan
a) 𝑥² - 5𝑥 + 4 = 0
b) 𝑥² + 7𝑥 + 12 = 0
c) 𝑥² - 6𝑥 - 7 = 0
d) 𝑥² + 2𝑥 - 24 = 0
Jawab:
a) 2𝑥² - 7𝑥 + 3 = 0
b) 6𝑥² - 5𝑥 - 6 = 0
Jawab:
a) Bagi persamaan dengan keofisien x^2 yaitu 2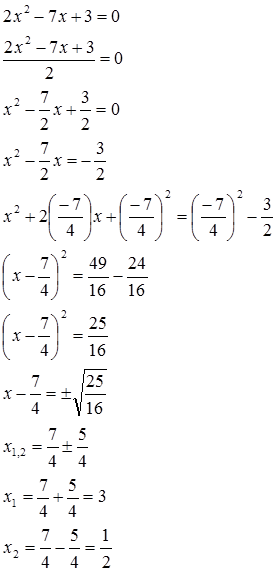 |
b) Bagi persamaan dengan keofisien x^2 yaitu 6 |





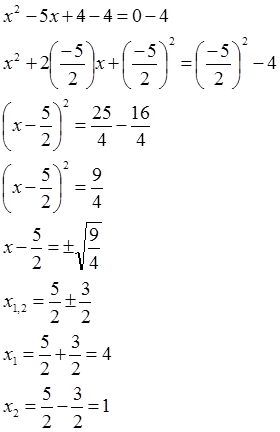

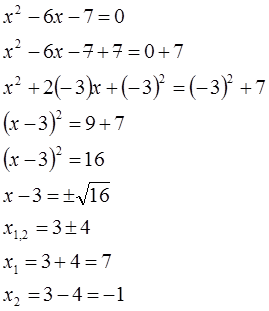
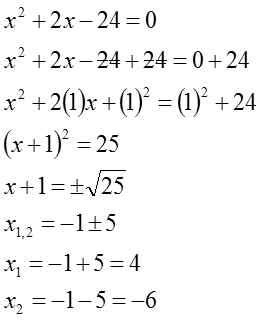









Spot on with this write-up, I honestly believe that this site
BalasHapusneeds a lot more attention. I’ll probably be back again to read through more, thanks for the advice!
You are welcome and thanks for visit my blog.
HapusGood article! We are linking to this great post on our website.
BalasHapusKeep up the great writing.
Thank You and gladly. May i know what is your site ?
HapusThis site was... how do I say it? Relevant!! Finally I have
BalasHapusfound something which helped me. Thanks!
You're welcome. Thanks for visit my blog.
HapusI love it whenever people come together and share views.
BalasHapusGreat website, continue the good work!
Thankyou.
HapusHaving read this I thought it was really informative.
BalasHapusI appreciate you taking the time and effort to put this
short article together. I once again find myself personally
spending a significant amount of time both reading and leaving comments.
But so what, it was still worth it!
Thank you
HapusGood blog you have got here.. It’s hard to find good quality writing like yours nowadays.
BalasHapusI truly appreciate individuals like you! Take care!!
Thank you
HapusOh my goodness! Incredible article dude! Many thanks, However I
BalasHapusam having troubles with your RSS. I don’t
know why I am unable to join it. Is there anyone else having the same RSS
issues? Anyone who knows the solution can you kindly respond?
Thanx!!
You're welcome. Thanks for visit my blog.
HapusAn outstanding share! I have just forwarded this onto a
BalasHapuscoworker who has been doing a little research on this.
And he actually bought me dinner because I found it for him...
lol. So let me reword this.... Thanks for the meal!! But yeah, thanx for spending some time
to discuss this issue here on your blog.
You're welcome. Thanks for visit my blog.
HapusEverything is very open with a really clear explanation of the challenges.
BalasHapusIt was truly informative. Your website is extremely helpful.
Thanks for sharing!
You're welcome. Thanks for visit my blog.
Hapus