Tip: Jika rumus tidak jelas pada tampilan mobile/hape, mintalah situs desktop/web pada browser Anda
Perhatikan permutasi dari tiga huruf $A, B$, dan $C$ yaitu
$ABC\quad ACB\quad BAC\quad BCA\quad CAB\quad CBA$
Kalau unsur-unsur yang tersedia boleh dituliskan berulang, maka diperoleh susunan huruf
$AAA\quad AAB\quad AAC\quad ABA\quad ABB\quad ABC\quad ACA\quad ACB\quad ACC $
$BAA\quad BAB\quad BAC\quad BBA\quad BBB\quad BBC\quad BCA\quad BCB\quad BCC $
$CAA\quad CAB\quad CAC\quad CBA\quad CBB\quad CBC\quad CCA\quad CCB\quad CCC $
Permutasi semacam ini disebut permutasi berulang (repeated permutation). Berdasarkan kaidah perkalian, banyak permutasi berulang 3 unsur yang diambil dari 3 unsur berbeda di atas adalah $3×3×3 = 27$.
Misalkan terssedia $n$ unsur berbeda. Banyaknya permutasi berulang $r$ unsur yang dianbil dari $n$ unsur yang tersedia adalah
Contoh 1
Berapa banyak susunan dua huruf yang diambil dari huruf-huruf $B, A, G, U$ dan $S$, kalau unsur-unsur yang tersedia boleh berulang
Jawab: Banyak unsur $n=5$, susunan terdiri dari 2 huruf ( $r =2$).
Jadi, terdapat 25 susunan dua huruf yang di antaranya mengandung beberapa huruf berulang.
Contoh 2
Berapa banyak bilangan yang terdiri dari tiga angka yang diambil dari angka-angka 1, 4, 3, 9, kalau angka-angka boleh berulang ?.
Jawab: Banyak unsur $n=4$, susunan terdiri dari 3 angka ( $r =3$)
Jadi, terdapat 64 bilangan tiga angka yang di antaranya mengandung beberapa angka berulang.
Topik terkait:
Kaidah pencacahan-Pengisian Tempat
Notasi faktorial
Permutasi Unsur-unsur Berbeda
Permutasi Unsur-unsur Sama
Permutasi Siklis
Kombinasi

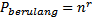












Tidak ada komentar:
Posting Komentar