
Ilustrasi Program linear

A. Pengertian Program linear
Program linear adalah sebuah perencanaan untuk mencapai nilai optimum yang bisa berupa nilai maksimum atau minimum dari suatu tantangan (fungsi objektif/tujuan) yang mempunyai kendala-kendala dalam bentuk sistem pertidaksamaan linear (pangkat 1) dua variabel (atau lebih) dengan keterangan tambahan lainnya dari variabel-variabel yang terlibat (lihat contoh-contoh).
Bentuk masalah program linear banyak berbentuk soal cerita dalam kehidupan sehari-hari yang berkaitan dengan perekonomian, namun ada juga yang tidak berkaitan dengan perekonomian.
Untuk menyelesaikan masalah program linear yang berbentuk soal cerita terlebih dahulu harus dibuat model matematika permasalahannya. Sedangkan untuk menyelesaikan masalah program linear yang berbentuk konsep, bisa diselesaikan dengan melakukan penyelidikan yang diperlukan. Artikel ini juga memuat contoh- contoh soal cerita program linear dan contoh soal program linear metode grafik.
Jika digambarkan secara geometri , program linear terkait dengan bentuk persamaan garis lurus, antara lain :
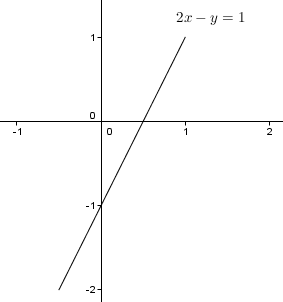
- $y – y_1 = m(x – x_1)$ : Garis yang bergradien m dan melalui titik $(x_1, y_1)$.
Contoh. Garis yang bergradien 2 dan melewati (1, 1) adalah $y-1=2(x-1)⟺2x-y=1$
- $qx + py = pq$ : Garis yang memotong sumbu x di (p, 0) dan sumbu y di (0, q).
Contoh. Garis yang memotong sumbu x di (4, 0) dan sumbu y di (0, 3) adalah $3x+4y=12$
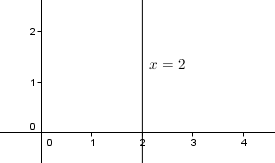
- $x=k$: Garis yang memotong sumbu x di (k, 0) dan tidak memotong sumbu y
Contoh. Garis yang memotong sumbu x di (2, 0) adalah x=2
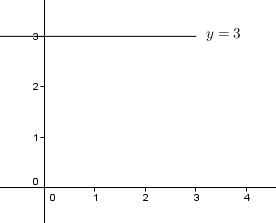
- $y=l$: Garis yang memotong sumbu y di (0, l) dan tidak memotong sumbu x
Contoh. Garis yang memotong sumbu y di (0, 3) adalah y=3
Oleh karena itu penggambaran masalah program linear secara geometri sangat membantu dalam mencari penyelesaian masalah program linear yang berupa nilai optimum atau minimum dari fungsi objektif.
B. Persiapan model matematika
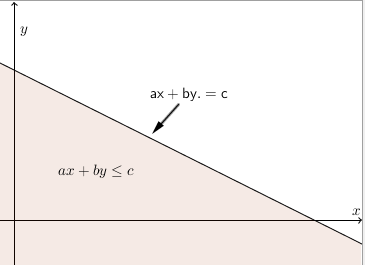
-Menentukan daerah arsiran dari suatu pertidaksamaan linear.
Untuk $ ax + by <= c$
Untuk $ax + by >= c$
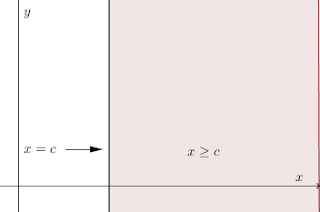
Untuk $x>=c$
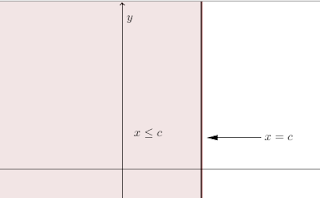
Untuk $x<=c$
Untuk $y>= c$
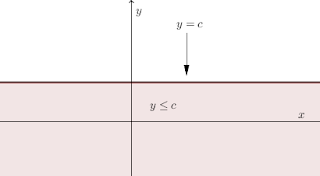
Untuk $y<= c$
-Menentukan daerah arsiran dari banyak pertidaksamaan.
Daerah arsiran dari banyak pertidaksamaan adalah daerah irisan dari semua pertidaksamaan.
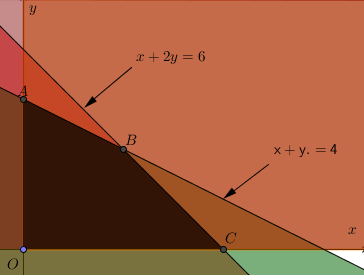
Contoh1. Buatlah grafik daerah penyelesaian sistem pertidaksamaan
Jawab
daerah penyelesaiannya adalah daerah OABC yang merupakan daerah irisan semua pertidak samaan
Contoh 2. Buatlah grafik daerah penyelesaian sistem pertidaksamaan
Jawab
daerah penyelesaiannya adalah daerah ABCD yang merupakan daerah irisan semua pertidak samaan
C. Membuat Model matematika
Untuk membuat model matematika dari soal cerita gunakan langkah-langkah bikut:
-buat pemisalan kuantitas-kuatitas yang diketahui ke dalam variabel-variabel agar lebih mudah diamati
-buat tabel perencanaan model matematika (jika diperlukan).
-Model matematika terdiri atas :
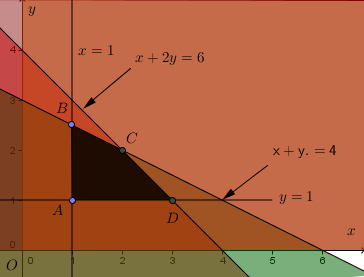
Batasan / Kendala :
Dua kendala
Tiga kendala
Dengan k1 dank2 blangan-bilangan nonnegatif
Fungsi obyektif $z = f( x, y) = px + qy$ maximum/ minimum:
-Melukis grafik daerah himpunan penyelesaian (dari batasan)
-Menentukan titik-titik potong pada daerah penyelesaian).
-memasukan titik-titik potong ke dalam fungsi objektif sehingga didapat jawab optimal.
Contoh 3. contoh soal cerita program linear
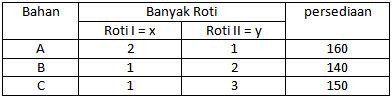
Seorang tukang roti mempunyai bahan A, B, dan C masing-masing sebanyak 160 kg, 140 kg, dan 150 kg.
Roti I memerlukan 2 kg bahan A, 1 kg bahan B, dan 1 kg bahan C.
Roti II memerlukan 1 kg bahan A, 2 kg bahan B, dan 3 kg bahan C.
Roti I dijual dengan harga Rp 10.000,00 dan Roti II dijual dengan harga Rp 20.000,00. Pendapatan maksimum yang dapat diperoleh tukang roti tersebut adalah….
Pembahasan :
Misalnya banyak roti I = x buah dan banyak roti II = y buah.
Perhatikan tabel di bawah
Dengan melihat tabel maka model matematika yang sesuai adalah
Fungsi Pendapatan $f(x,y)=10000x+20000y$ .
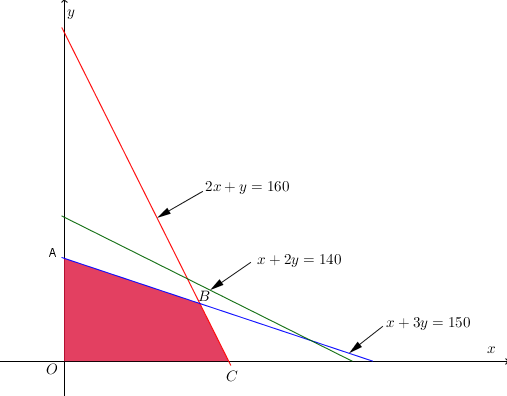
Grafik
-Koordinat titik O adalah (0,0)
-Koordinat titik A diperoleh dengan memasukan x=0 ke persamaan x+3y=150.
jadi koordinat titik A (0,50).
-Koordinat titik B adalah perpotongan garis 2x+y=160 dan x+3y=150.
Dengan metode determinan Crammer
jadi koordinat titik B(66,28).
- Koordinat titik C diperoleh dengan memasukan y=0 ke persamaan 2x+y=160.
jadi koordinat titik C(80,0).
Masukkan semua ttik potong pada fungsi objektif.
f(0,0)=0
f(0,50)=10.000×0 + 20.000×50 = 1000.000
f(66,28)=10.000×66 + 20.000×28 = 1220.000
f(80,0)=10.000×80 + 20.000×0 = 800.000
Jadi, pendapatan maksimum yang dapat diperoleh tukang roti itu adalah Rp 1.220.000
D. Metode Grafik
Untuk memperoleh nilai optimum (maksimum atau minimum) dari fungsi obyektif dengan kendala-kendala tertentu, dapat kita lakukan dengan menggambar daerah penyelesaian layak yaitu daerah yang titik-titiknya merupakan himpunan penyelesaian dari sistem pertidaksamaan linier. Kemudian nilai optimum dari fungsi obyektif akan dicari menggunakan garis selidik.
pengertian garis selidik.
Jika fungsi obyektik dari suatu masalah adalah f = ax + by, maka garis selidik nya adalah ax + by = k, untuk beberapa nilai k, dengan k e R. Untuk memahami pengertian garis selidik perhatikan contoh berikut.
Contoh 4. contoh soal program linear metode grafik
Diketahui fungsi obyektif dari suatu masalah adalah f = 2x + 3y. Buatlah garis selidik dengan menggunakan fungsi tujuan.
Penyelesaian
Garis selidiknya adalah 2x + 3y = k,
Untuk k = 0, 6, 12 didapat:
- garis 2x + 3y = 0, garis ini disebut garis senilai, sebab untuk (x,y) yang memenuhi garis itu nilai f selalu sama yaitu 0.
- garis 2x + 3y = 6, garis ini disebut garis senilai, sebab untuk (x,y) yang memenuhi garis itu nilai f selalu sama yaitu 6.
-garis 2x + 3y = 12, garis ini disebut garis senilai, sebab untuk (x,y) yang memenuhi garis itu nilai f selalu sama yaitu 12.
Tiga garis senilai yang di lukis di atas diperlukan guna menyelidiki kemiringan garis senilai dan arah pergeserannya maka ketiga garis senilai secara bersama-sama disebut garis selidik.
Dari contoh di atas ternyata:
a) garis selidik makin menjauhi (0,0) (atau ke kanan/ke atas) jika nilai k bertambah besar atau sebaliknya.
b) garis selidik selalu sejajar atau gradiennya sama dan disini gradiennya -2/3.
.
Contoh 5. contoh soal program linear metode grafik
Dengan menggunakan garis selidik, tentukan x dan y yang memaksimumkan f= 4x + 3y, dengan kendala
3x + 4y <= 12
7x + 2y <= 14
x >=0
y >= 0
Penyelesaian
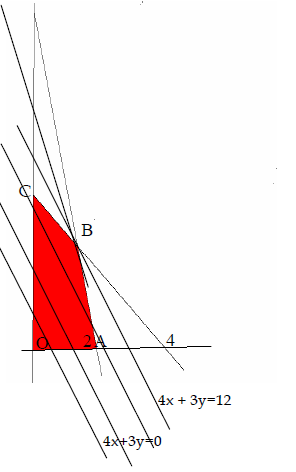
- Untuk k = 0 didapat garis senilai 4x + 3y = 0,
- Untuk k = 12 didapat garis senilai 4x + 3y = 12,
Ternyata garis selidik makin menjauhi (0,0) jika nilai f makin besar.
Setelah digambar himpunan daerah penyelesaiannya adalah daerah tertutup OABC, dengan O(0,0),A(2,0), B(16/11,21/11) yang merupakan titik potong garis 3x + 4y = 12 dan7x + 2y =14, dan C (0,3).
Jika garis selidik digerakkan ke atas/kanan dengan bantuan dua penggaris siku-siku maka nilai f makin besar, dan nilai f paling besar saat garis selidik menyinggung daerah himpunan penyelesaian yang paling luar, yaitu titik B. Jadi nilai maksimum f= 4(16/11)+ 3(21/11)=127/11
untuk x = 16/11 dan y =21/11
E. Contoh tambahan dan Pembahasan
1. Perusahaan pengiriman barang mempunyai dua jenis mobil yaitu jenis I dan II. Mobil jenis I daya muatnya 12 m3, sedangkan mobil jenis II daya muatnya 36 m3. Order tiap bulan rata–rata mencapai lebih dari 7.200 m3, sedangkan biaya per pengiriman untuk mobil jenis I Rp400.000,00 dan mobil jenis II Rp600.000,00. Dari biaya yang telah ditetapkan tersebut pendapatan rata–rata sebulan tidak kurang dari Rp200.000.000,00. model matematika yang tepat dari masalah tersebut adalah …
A. x + 3y >= 600, 2x + 3y >= 1000, x >= 0, y >= 0
B. x + 3y >= 600, 2x + 3y <= 1000, x >= 0, y >= 0
C. x + 3y >= 400, 2x + 3y >= 2000, x >= 0, y >= 0
D. x + 3y >= 400, 2x + 3y <= 2000, x >= 0, y >= 0
E. x + 3y >= 800, 2x + 3y >= 1000, x >= 0, y >= 0
Pembahasan :
Misalkan mobil jenis I = x dan mobil jenis II = y.
Daya muat – order : 12x+36y≥7200⟹x+3y≥600.
Biaya – pendapatan : 400.000x+600.000y≤200.000.000⟹2x+3y≤1000.
x >= 0, y >= 0 solusi non negatif, karena banyak mobil tidak negatif.
Jawaban B.
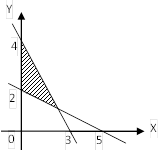
2. Daerah yang diarsir pada gambar berikut merupakan himpunan penyelesaian system pertidaksamaan …
A. 2x + 5y <= 10, 4x + 3y <= 12, x <= 0, y <= 0
B. 2x + 5y <= 10, 4x + 3y >= 12, x <= 0, y <= 0
C. 2x + 5y <= 10, 4x + 3y <= 12, x >= 0, y >= 0
D. 2x + 5y >= 10, 4x + 3y >= 12, x >= 0, y >= 0
E. 2x + 5y >= 10, 4x + 3y <= 12, x <= 0, y <= 0
Pembahasan :
Garis I: 4x+3y=12 daerah arsiran ada di bawah garis 1 maka 4x+3y≤12.
Garis II: 2x+5y=10 daerah arsiran ada di atas garis II maka 2x+5y≥10.
x≥0,y≥0. Solusi non negatif.
Jawaban E.
- contoh soal cerita program linear
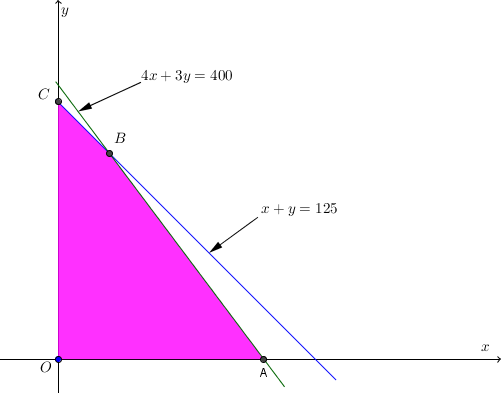
3. Di atas tanah seluas 1 hektar akan dibangun dua tipe rumah, yaitu tipe A dan tipe B. Tiap unit rumah tipe A luasnya 100 m2, sedangkan tipe B luasnya 75m2. Jumlah rumah yang akan dibangun paling banyak 125 unit. Harga jual rumah tipe A adalah Rp100.000.000 dan rumah tipe B adalah Rp60.000.000. Supaya pendapatan dari hasil penjualan seluruh rumah maksimum, maka harus dibangun rumah sebanyak ….
A. 100 rumah tipe A saja
B. 125 rumah tipe A saja
C. 100 rumah tipe B saja
D. 100 rumah tipe A dan 25 tipe B
E. 25 rumah tipe A dan 100 tipe B
Pembahasan :
Misalkan rumah tipe A = x dan rumah tipe B = y. Diketahui 1 hektar = 10000 m2.
Luas rumah – luas tanah : $100x+75y≤10000⟹4x+3y≤400$…(1)
Banyak rumah : $x+y≤125$ …(2)
x≥0,y≥0 solusinon negatif. Karena banyak rumah tidak negatif.
Keuntungan : $f(x,y)=100.000.000x+60.000.000y$
- titik potong A
masukan y = 0 ke persamaan (1) maka x = 100. Titik A(100,0).
-titik potong B
Dari x+y=125 ambil x=125-y. Masukan x ini ke 4x+3y=400.
4(125-y)+3y=400
500-4y+3y=400
-y=-100
y=100.
Masukan y = 100 ke x+y=125 .
x+100=125
x=125-100=25
Titik B(25, 100)
- titik potong C
masukan x = 0 ke persamaan (2) maka y = 125. Titik C (0, 125).
-uji tiap titik pada fungsi keuntungan
f(100,0)=100.000.000(100)+60.000.000(0)=10.000.000.000
f(25,100)=100.000.000(25)+60.000.000(100)=8.500.000.000
f(0,125)=100.000.000(0)+60.000.000(125)=7.500.000.000
pendapatan dari hasil penjualan seluruh rumah maksimum, jika dibangun rumah tipe A sebanyak 100.
Jawaban A.
4. Bimbingan Alumni UI
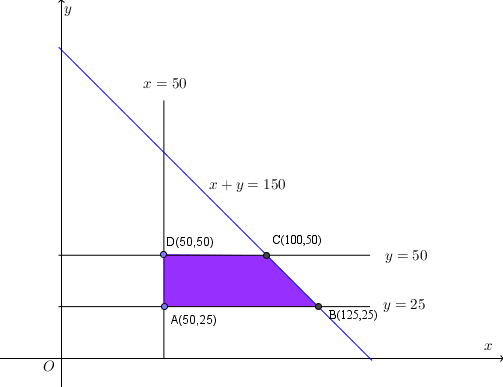
Seorang pemilik toko kue ingin mengisi tokonya dengan kue donat paling sedikit 50 buah dan kue bolu paling sedikit 25 buah. Toko tersebut dapat memuat 150 kue. Keuntungan kue bolu dua kali kue donat. Jika banyak kue bolu tidak melebihi 50 buah, maka agar untung maksimum banyak kue donat dan bolu adalah
(A) 125 donat dan 25 bolu
(B) 100 donat dan 50 bolu
(C) 25 donat dan 125 bolu
(D) 50 donat dan 100 bolu
(E) 150 donat
Pembahasan
Misalkan banyak kue donat = x, banyak kue bolu = y.
Keuntungan kue donat = d, Keuntungan kue bolu = b = 2d
fungsi objektif→$f(x,y)=dx+by=dx+2dy=(x+2y)d$
.f(50,25)=(50+50)d=100d
f(125,25)=(125+50)d=175d
f(100,50)=(100+100)d=200d
f(50,50)=(50+100)d
jawaban B..




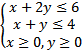
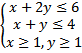



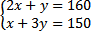












ka mau tanya no4, kenapa kue donatnya banyaknya ngga 200? kan dia maksimum
BalasHapus