Persamaan kuadrat adalah suatu persamaan dengan pangkat tertinggi pada variabelnya sama dengan dua. Umumnya persamaan kuadrat memuat tiga suku yaitu suku pertama adalah suku yang memuat variabel berpangkat dua, suku kedua adalah suku yang memuat variabel berpangkat satu, dan suku ketiga adalah suku yang memuat bilangan tetap atau konstanta.
Bentuk umum atau bentuk baku persamaan kuadrat dalam variabel x adalah sebagai berikut
Dimana:
a, b, c adalah bilangan real.
a disebut koefisien (pengali) x², a ≠ 0.
a disebut koefisien (pengali) x², a ≠ 0.
b disebut koefisien (pengali) x.
c disebut konstanta (tetapan).
Contoh 1. Tentukan mana persamaan kuadrat dan yang bukan. Jika persamaan kuadrat tentukan pula koefisien a, b dan konstanta c.
1) 4x² + 2x + 3 = 0
2) 3x² - 2x = 0
3) 2x² - 5 = 0
4) 2x + 3 = 0
5) x³ - 4x² + 2x + 3 = 0
Jawab:
1) Pesamaan kuadrat. Koefisien a = 4, koefisien b = 2 dan konstanta c = 3.
2) Pesamaan kuadrat. Disini konstanta c tidak muncul, itu artinya konstanta c = 0 seperti dijelaskan berikut
3x² - 2x = 0
⟺ 3x² + (-2)x + 0 = 0
Maka koefisien a = 3, koefisien b = -2 dan konstanta c = 0.
3) Pesamaan kuadrat. Disini koefisien b tidak muncul, itu artinya koefisien b =0 seperti dijelaskan berikut
2x² - 5 = 0
⟺ 2x² + 0x + (-5) = 0
Maka koefisien a = 2, koefisien b = 0 dan konstanta c = -5.
4) Bukan pesamaan kuadrat karena pangkat tertingginya 1.
5) Bukan pesamaan kuadrat karena pangkat tertingginya 3.
Contoh 2. Ubahlah persamaan-persamaan kuadrat berikut ke dalam bentuk umum persamaan kuadrat. Tentukan koefisien a, b dan konstanta c.
Jawab:
Contoh 3. Ubahlah persamaan-persamaan fungsi rasional (pecahan) berikut ke dalam bentuk umum persamaan kuadrat. Tentukan koefisien a, b dan konstanta c.
Jawab:
Untuk menentukan akar-akar persamaan kuadrat digunakan metode-metode antara lain: metode pemfaktoran, melengkapkan kuadrat sempurna, dan pemakaian rumus akar kuadrat yang sering disebut rumus abc.

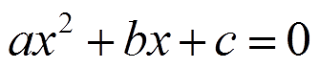
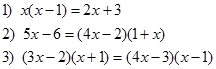

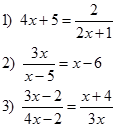
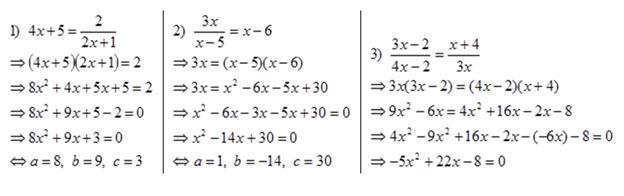









Tidak ada komentar:
Posting Komentar