Minggu, 25 November 2018

Limit Fungsi-Definisi Formal, Metode Pembuktian dan Sifat-sifat Limit

Misalkan diberikan fungsi f(𝑥) = 𝑥². Amati nilai f(𝑥) pada sumbu y bila 𝑥 mendekati 2 pada sumbu x. pada saat itu perhatikan bahwa f(𝑥) mendekati suatu nilai tertentu.

Fokus perhatian kita adalah pada sumbu y, bukan pada f(𝑥) = 𝑥². perlu diketahui pula bahwa mendekati 2 pada contoh ini adalah mendekati dari kiri dan kanan karena fungsi terdefinisi di 𝑥 < 2 dan 𝑥 > 2.

Mencermati ilustrasi tersebut adalah wajar bila kita simpulkan f(𝑥) mendekati 4 jika 𝑥 mendekati 2, dengan kata lain 4 adalah limit atau batas untuk f(𝑥) saat 𝑥 mendekati 2 . Nilai 4 yang didekati oleh f(𝑥) saat 𝑥 mendekati 2 tak ada kaitannya dengan nilai f(2)=4. Bahkan seandainya f(2) tidak terdefinisi, f(𝑥) tetap mendekati 4 saat 𝑥 mendekati 2. Hal ini dalam matematika ditulis dalam bentuk simbolis sebagai

Kalau kita buat versi Indonesianya begini

Hehe…

Definisi formal limit

Misalkan f(𝑥) didefinisikan dan bernilai tunggal untuk semua nilai 𝑥 di dekat 𝑥 = a dengan pengecualian yang mungkin dari 𝑥 = a itu sendiri (yakni dalam tetangga δ yang dicoret dari a). Kita katakan bahwa bilangan L adalah limit f(𝑥) jika 𝑥 mendekati a dan kita tuliskan

Jika untuk setiap bilangan positif ϵ (baca: epsilon) pada ordinat, bagaimanapun kecilnya. Kita bisa mencari bilangan positif δ (baca: delta) pada absis sehingga

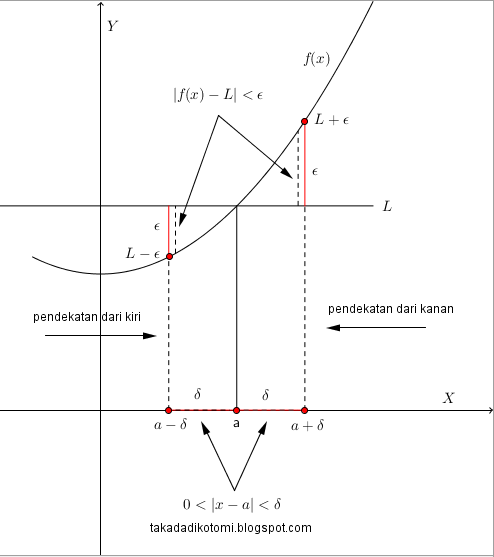ilustrasi definisi limit yang memuat limit kanan dan limit kiri

keterangan gambar:

✦ ϵ (epsilon) dan δ (delta) adalah garis-garis berwarna merah

✦ |𝑥-a| adalah garis putus-putus berimpit dengan δ (delta)

✦ |f(𝑥)-L| adalah garis putus-putus di sebelah kanan atau kiri ϵ (epsilon).

✦ pada pendekatan dari kanan atau limit kanan, bulatan pada sumbu-x menyatakan 𝑥 ≠ a dan 𝑥 ≠ a+δ dan pada sumbu-y menyatakan f(𝑥) ≠ L+∈

✦ pada pendekatan dari kiri atau limit kiri, bulatan pada sumbu-x menyatakan 𝑥 ≠ a dan 𝑥 ≠ a-δ dan pada sumbu-y menyatakan f(𝑥) ≠ L-∈

Dalam kata-kata, ini berarti bahwa kita dapat membuat nilai mutlak dari selisih f(x) dan L sekecil yang kita inginkan dengan memilih x sangat dekat ke a, yaitu dengan memilih nilai mutlak dari selisih x dan a sangat kecil tetapi tidak nol.

Langkah-langkah pembuktian limit dengan definisi

Langkah 1: tetapkan delta sebagai suatu nilai positif (misalnya 1). Tentukan selang penyelesaian pertidaksamaan nilai mutlak yang memuat delta sebagai berikut

Langkah 2: tentukan hubungan epsilon - delta dengan mengganti suku |𝑥-a| oleh δ dan variabel 𝑥 pada suku-suku yang tersisa oleh nilai real a+δ pada persamaan sementara

Hubungan epsilon - delta ini diperlukan jika kita ingin menunjukkan berapa nilai delta yang harus diambil agar |f(𝑥)-L|<ϵ

Langkah 3: menyatakan bukti

Contoh 1. Buktikan bahwa

Jawab:

Kita harus memperlihatkan bahwa diberikan sembarang ϵ > 0 maka kita dapat mencari δ > 0 sehingga |𝑥² - 4|<ϵ bila 0<|𝑥 - 2|<δ.

- Pilihlah δ sebagai suatu bilangan positif sehingga

0<|𝑥-2|<δ

2-δ<𝑥<2+δ; 𝑥≠2

Misalnya bilangan positif itu 1.

0<|𝑥-2|<1.

1<𝑥<3, 𝑥≠2.

- Cari hubungan epsilon-delta. Ganti suku |𝑥-2| oleh δ dan 𝑥 pada suku yang tersisa oleh nilai 2+δ=3

- Bukti. Ambilah δ<1 atau ϵ/5 yang mana saja di antara yang lebih kecil. Maka kita memperoleh |𝑥² - 4|<ϵ bila 0<|𝑥 - 2|<δ dan hasil yang diperlukan pun sudah dibuktikan.

Beberapa nilai numerik mungkin diperlukan agar lebih mudah dipahami. Misalnya jika kita ingin membuat |𝑥² - 4|<0,05 maka kita bisa memilih δ=ϵ/5=0,05/5=0,01.

Perhatikan, sekarang kita periksa apakah dengan mengambil δ=0,01 benar membuat |𝑥² - 4|<0,05.

0<|𝑥 - 2|<0,01

1,99<𝑥<2,01;𝑥≠2

1,99²<𝑥²<2,01²

1,99² - 4<𝑥² - 4<2,01² - 4

1,99² - 2²<𝑥² - 4<2,01² - 2²

3,99(-0,01)<𝑥² - 4<4,01(0,01)

-0,0399<𝑥² - 4<0,0401

Perhatikan bahwa selang pertidaksamaan di atas berada dalam selang pertidaksamaan

-0,05<𝑥² - 4<0,05

Jadi, dengan mengambil δ=0,01 benar membuat |𝑥² - 4|<0,05; 𝑥²≠4

Contoh 2. Buktikan bahwa

Jawab:

Kita harus memperlihatkan bahwa diberikan sembarang ϵ>0 maka kita dapat mencari δ>0 sehingga |𝑥⁴ - 81|<ϵ bila 0<|𝑥-3|<δ.

- Pilihlah δ sebagai suatu bilangan positif sehingga

0<|𝑥-3|<δ

3-δ<𝑥<3+δ; 𝑥≠3

Misalnya bilangan positif itu 1.

0<|𝑥-3|<1

2<𝑥<4; 𝑥≠3

- Cari hubungan epsilon delta. Gantikan suku |𝑥-3| oleh δ dan 𝑥 pada suku-suku yang tersisa oleh nilai 3+δ=4.

|𝑥⁴ - 81|=ϵ

|(𝑥²+9)(𝑥²-9)|=ϵ

|(𝑥²+9)(𝑥+3)(𝑥-3)|=ϵ

|𝑥²+9||𝑥+3||𝑥-3|=ϵ

|4²+9||4+3|δ=ϵ

175δ=ϵ

⟹δ=ϵ/175

- Bukti. Ambilah δ<1 atau ϵ/175 yang mana saja di antara yang lebih kecil. Maka kita memperoleh |𝑥⁴ - 81|<ϵ bila 0<|𝑥-3|<δ dan hasil yang diperlukan pun sudah dibuktikan.

Beberapa nilai numerik mungkin diperlukan agar lebih mudah dipahami. Misalnya jika kita ingin membuat |𝑥⁴ - 81|<0,05 maka kita bisa memilih δ=0,05/175=1/3500.

Perhatikan, sekarang kita periksa apakah dengan mengambil δ=1/3500 benar membuat |𝑥⁴ - 81|<0,05.

Perhatikan, selang pertidaksamaan di atas ada dalam selang

Jadi, dengan mengambil δ=1/3500 benar membuat |𝑥⁴ - 81|<0,05; 𝑥⁴≠81

Selanjutnya, jika kita ingin membuat |𝑥⁴ - 81|<0,01 maka kita bisa memilih δ=0,01/175=1/17500, dan seterusnya.

Limit kanan dan limit kiri

Dalam definisi limit tidak dibuat batasan mengenai bagaimana 𝑥 seharusnya mendekati a. dengan meninjau 𝑥 dan a sebagai titik-titik pada sumbu real dimana 𝑥 bergerak dan a tetap, maka 𝑥 dapat mendekati a dari kanan atau kiri. Dua pendekatan tersebut lazim ditulis sebagai 𝑥→a⁺ dan 𝑥→a^-.

Jika

dan

maka L⁺ dinamakan limit kanan dan L^- limit kiri dari f(x) di x=a dan menyatakannya dengan f(a⁺ ) atau f(a+0) dan f(a^-) atau f(a - 0). Definisi epsilon-delta dari limit f(x) untuk x→a⁺ dan x→a^- adalah sama seperti untuk definisi x→a hanya saja nilai-nilai x dibatasi. Dan yang menjadi dasar adalah bahwa

jika dan hanya jika

Sifat-sifat Limit

Dalam menentukan nilai limit suatu fungsi, kita tidak harus menggunakan definisi limit tetapi memanfaatkan teorema-teorema limit. Berikut adalah beberapa teorema atau sifat yang digunakan untuk mentukan nilai suatu limit.

Jika