A. Limit fungsi f(x) untuk x menuju nilai tertentu (x→a,a∈R)
1. Substitusi langsung pada fungsinya
Misalkan ingin diketahui hasil limit f(x) saat x mendekati c. Jika f(c) tidak tak terdefinisi atau tidak tak tentu atau tidak tak hingga, maka umumnya nilai limit f(x) saat x mendekati c adalah f(c). Cara ini diperoleh dengan memanfaatkan kekontinyuan fungsi di titik c.Contoh
a)
b)
Jika fungsi tidak kontinyu di c maka cara ini tidak bisa digunakan.
Contoh
a)
tidak bisa substitusi langsung karena untuk x=1 fungsi memuat bentuk tak tentu 0/0.
b) Diberikan
Tentukan
Jawab:
Dari fungsi jelas f(4)=0 tetapi
. Jadi tidak berlaku
walaupun f(4) ada yaitu 0 ini tidak bisa memakai cara substitusi langsung.
2. Menyederhanakan bentuk rasional
Cara ini diperoleh dengan membagi faktor yang sama pada pembilang dan penyebut.Contoh
a)
b)
3. Modifikasi bentuk k/0 dengan k ≠ 0.
Contoh
Bentuk ini memuat 2/0 dan 1/0 yaitu
meskipun begitu limitnya ada yaitu
4 Aturan L’Houpital untuk bentuk 0/0
Contoha)
Dengan menggunakan aturan L’Houpital, pembilang dan penyebut diturunkan terhadap x (lihat turunan)
b)
Memuat bentuk 0/0 untuk x=4 hanya pada suku
Gunakan aturan L’Houpital pada suku itu saja tidak perlu diterapkan pada yang lainnya.
B. Limit fungsi f(x) untuk x menuju tak hingga
1. Limit fungsi yang memuat bentuk ∞-∞
Untuk menyelesaikan limit yang memuat bentuk ∞-∞ dapat diselesaikan dengan mengalikan fungsi dengan fungsi pecahan dimana pembilang dan penyebutnya adalah sekawan (conjugate) fungsi tersebut.Contoh
a)
b)
2. Limit fungsi yang memuat bentuk ∞/∞
Untuk menentukan Limit fungsi yang memuat bentuk ∞/∞, bagi pembilang dan penyebut oleh pangkat tertinggi penyebut. Perlu diperhatikan polinomial yang memuat bentuk ∞/∞ ada tiga macam yaitu:- Pangkat tertinggi variabel pembilang lebih tinggi dari pangkat tertinggi variabel penyebut, maka limitnya tak hingga.
Contoh
- Pangkat tertinggi variabel pembilang lebih rendah dari pangkat tertinggi variabel penyebut, maka limitnya 0.
Contoh
- Pangkat tertinggi variabel pembilang sama dengan pangkat tertinggi variabel penyebut, maka limitnya adalah hasil bagi koefisien variabel tertinggi pembilang dengan koefisien variabel tertinggi penyebut.
Contoh

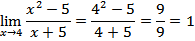
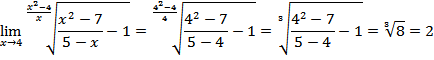
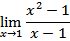
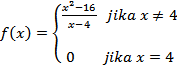

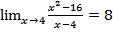

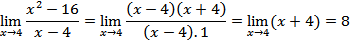
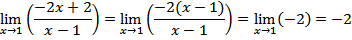

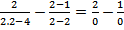
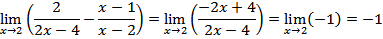
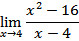
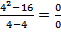
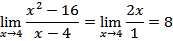
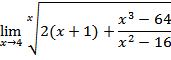
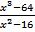
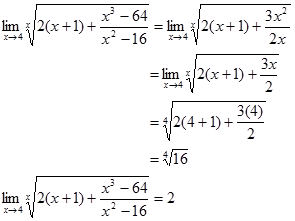
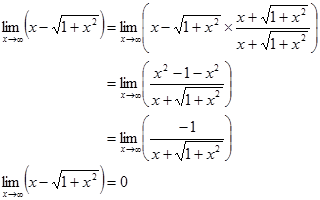
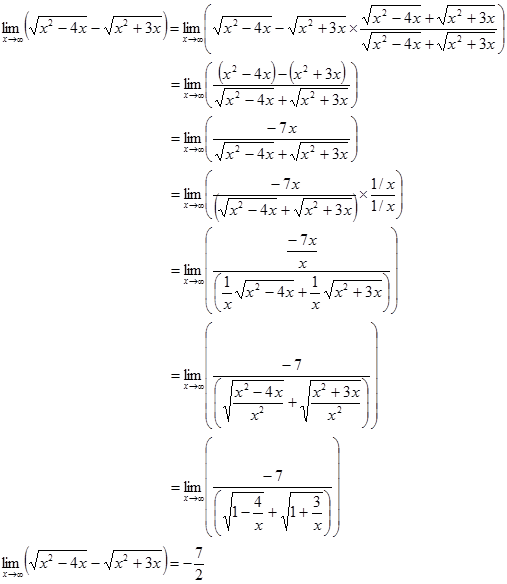
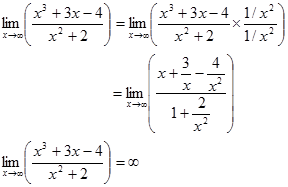
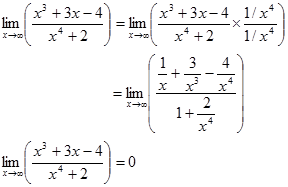
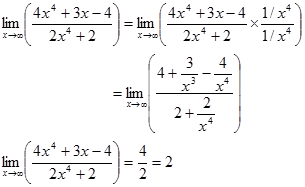









Tidak ada komentar:
Posting Komentar