Pertambahan suatu variabel 𝑥 dilambangkan dengan ∆𝑥 adalah perubahan dalam 𝑥 bila 𝑥 membesar atau mengecil dari suatu nilai awal 𝑥 = 𝑥₀ menjadi nilai berikutnya 𝑥 = 𝑥₁ pada jangkauannya, dalam hal ini ∆𝑥 = 𝑥₁ - 𝑥₀.
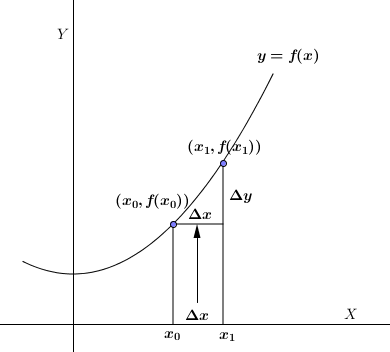
Bila variabel 𝑥 diberi pertambahan sebesar ∆𝑥, maka suatu fungsi y = f(𝑥) juga akan menerima perubahan dalam y sebesar
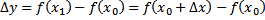
Hasil bagi
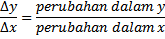
disebut laju perubahan rata-rata fungsi pada selang 𝑥 = 𝑥₀ dan 𝑥 = 𝑥₁= 𝑥₀ + ∆𝑥.
Turunan
Turunan atau derivative suatu fungsi y = f(𝑥) di titik 𝑥 = 𝑥₀ adalah limit laju perubahan rata-rata fungsi saat ∆𝑥 mendekati nol tetapi tidak nol dan didefinisikan sebagai
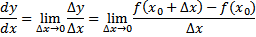
Asalkan limitnya ada.
Contoh 1. Cari turunan y = f(𝑥) = 𝑥² +1 pada 𝑥 = 𝑥₀. Hitung nilai turunan pada
a) 𝑥₀ = 2,
b) 𝑥₀ = 3.
Jawab:
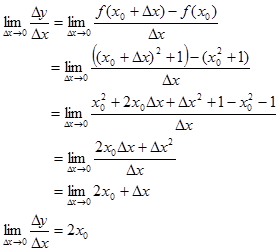
a) di 𝑥₀ = 2 nilai turunan adalah 2.2 = 4.
b) di 𝑥₀ = 3 nilai turunan adalah 2.3 = 6
Dalam mencari turunan suatu fungsi, indeks 0 biasanya dihilangkan dan turunan y = f(𝑥) terhadap 𝑥 dituliskan dengan
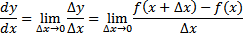
Beberapa notasi lain yang sering digunakan untuk turunan antara lain
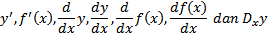
Contoh 2. Cari dy/d𝑥 jika y = 𝑥³ + 𝑥² -5. Berapa nilai dy/d𝑥 di 𝑥 = 4, 𝑥= 0, dan 𝑥 = -1 ?
Jawab:
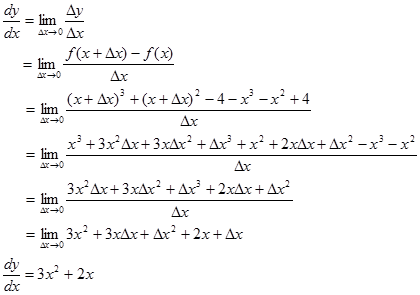
Notasi untuk dy/d𝑥 di 𝑥 = a bisa ditulis sebagai
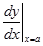
jadi
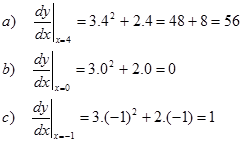
Contoh 3. Cari y’ jika y = (𝑥-1)/(𝑥+1). Berapa nilai y’ di 𝑥 = 0, 𝑥 = 1, dan 𝑥 = -1 ?
Jawab:
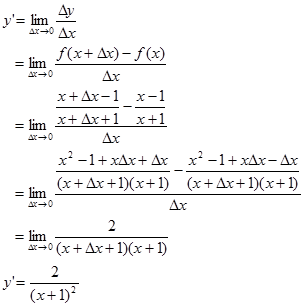
y’ di 𝑥 = 0 adalah $y'(0)=\frac{2}{(0+1)^2}=2$
y’ di 𝑥 = 1 adalah $y'(1)=\frac{2}{(1+1)^2}=\frac{1}{2}$
y’ di 𝑥 = -1 tidak ada
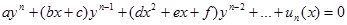
Dengan $u_{n}(x)$ adalah suatu polinomial dalam $x$.
Contoh. fungsi kuadrat $y = x^{2} – 10x+25$. Dari fungsi ini maka didapat $n=2, a=0, b=0, c=1, d=-1, e=10, f=-25$, dan $u_{3}(x)=u_{4}(x)=…=u_{n}(x)=0$.
Turunan fungsi aljabar dapat diperoleh dengan menerapkan definisi turunan fungsi pada fungsi-fungsi aljabar. Suatu fungsi aljabar (begitu juga fungsi transenden misalnya fungsi trigonometri) dapat diturunkan di $x = a $ jika fungsi itu mempunyai turunan di titik tersebut. Suatu fungsi aljabar dapat diturunkan pada suatu selang jika fungsi itu mempunyai turunan di setiap titik pada selang tersebut.
Dapat disimpulkan bahwa operator d/dx bersifat linear pada penjumlahan fungsi
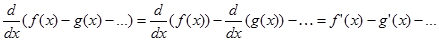

Bila variabel 𝑥 diberi pertambahan sebesar ∆𝑥, maka suatu fungsi y = f(𝑥) juga akan menerima perubahan dalam y sebesar
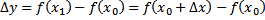
Hasil bagi
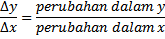
disebut laju perubahan rata-rata fungsi pada selang 𝑥 = 𝑥₀ dan 𝑥 = 𝑥₁= 𝑥₀ + ∆𝑥.
Turunan
Turunan atau derivative suatu fungsi y = f(𝑥) di titik 𝑥 = 𝑥₀ adalah limit laju perubahan rata-rata fungsi saat ∆𝑥 mendekati nol tetapi tidak nol dan didefinisikan sebagai
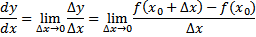
Asalkan limitnya ada.
Contoh 1. Cari turunan y = f(𝑥) = 𝑥² +1 pada 𝑥 = 𝑥₀. Hitung nilai turunan pada
a) 𝑥₀ = 2,
b) 𝑥₀ = 3.
Jawab:
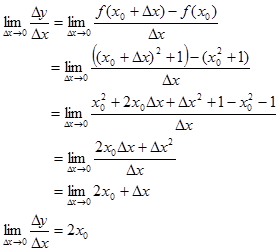
a) di 𝑥₀ = 2 nilai turunan adalah 2.2 = 4.
b) di 𝑥₀ = 3 nilai turunan adalah 2.3 = 6
Dalam mencari turunan suatu fungsi, indeks 0 biasanya dihilangkan dan turunan y = f(𝑥) terhadap 𝑥 dituliskan dengan
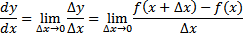
Beberapa notasi lain yang sering digunakan untuk turunan antara lain
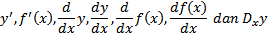
Contoh 2. Cari dy/d𝑥 jika y = 𝑥³ + 𝑥² -5. Berapa nilai dy/d𝑥 di 𝑥 = 4, 𝑥= 0, dan 𝑥 = -1 ?
Jawab:
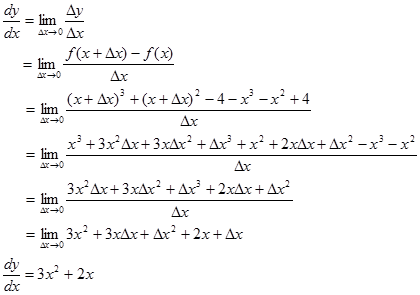
Notasi untuk dy/d𝑥 di 𝑥 = a bisa ditulis sebagai
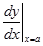
jadi
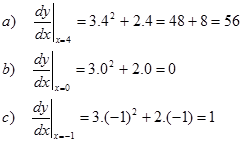
Contoh 3. Cari y’ jika y = (𝑥-1)/(𝑥+1). Berapa nilai y’ di 𝑥 = 0, 𝑥 = 1, dan 𝑥 = -1 ?
Jawab:
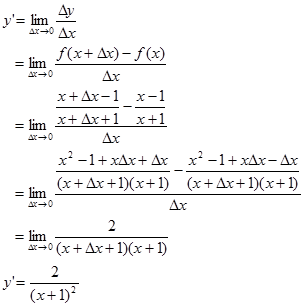
y’ di 𝑥 = 0 adalah $y'(0)=\frac{2}{(0+1)^2}=2$
y’ di 𝑥 = 1 adalah $y'(1)=\frac{2}{(1+1)^2}=\frac{1}{2}$
y’ di 𝑥 = -1 tidak ada
Turunan fungsi Aljabar
Suatu fungsi aljabar (bidang) adalah fungsi yang persamaannya dapat ditulis sebagai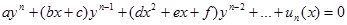
Dengan $u_{n}(x)$ adalah suatu polinomial dalam $x$.
Contoh. fungsi kuadrat $y = x^{2} – 10x+25$. Dari fungsi ini maka didapat $n=2, a=0, b=0, c=1, d=-1, e=10, f=-25$, dan $u_{3}(x)=u_{4}(x)=…=u_{n}(x)=0$.
Turunan fungsi aljabar dapat diperoleh dengan menerapkan definisi turunan fungsi pada fungsi-fungsi aljabar. Suatu fungsi aljabar (begitu juga fungsi transenden misalnya fungsi trigonometri) dapat diturunkan di $x = a $ jika fungsi itu mempunyai turunan di titik tersebut. Suatu fungsi aljabar dapat diturunkan pada suatu selang jika fungsi itu mempunyai turunan di setiap titik pada selang tersebut.
1. Turunan fungsi konstan
Misalkan $y =f(x) = c$, dengan $c$ sebuah konstanta sembarang maka

Bukti
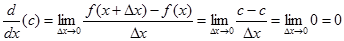
Contoh
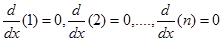

Bukti
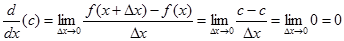
Contoh
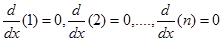
2. Turunan fungsi linear
Contoh. $y=4x+5⇒\frac{dy}{dx}=4$
3. Turunan fungsi pangkat
Dapat disimpulkan bahwa operator d/dx bersifat linear pada penjumlahan fungsi
5. Turunan pengurangan fungsi
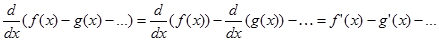
Dapat disimpulkan bahwa operator d/dx bersifat linear pada pengurangan fungsi

6. Turunan perkalian (dua) fungsi

Contoh

Bandingkan hasilnya dengan turunan fungsi $y=x^{4}-16$.
Turunan perkalian fungsi dapat diperluas untuk perkalian lebih dari dua fungsi misalnya tiga fungsi dengan menerapkan aturan perkalian dua fungsi secara berulang. Misalkan $f=f(x), g=g(x)$, dan $h=h(x)$.
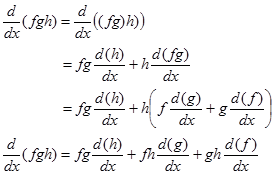

Bandingkan hasilnya dengan turunan fungsi $y=x^{4}-16$.
Turunan perkalian fungsi dapat diperluas untuk perkalian lebih dari dua fungsi misalnya tiga fungsi dengan menerapkan aturan perkalian dua fungsi secara berulang. Misalkan $f=f(x), g=g(x)$, dan $h=h(x)$.
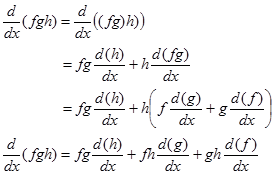
Contoh

Bandingkan hasilnya dengan turunan fungsi $y=x^{8}-32x^{4}+256$.
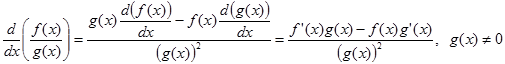
Contoh. Tentukan turunan $\frac{x^{4}-16}{x^{2}+4}$
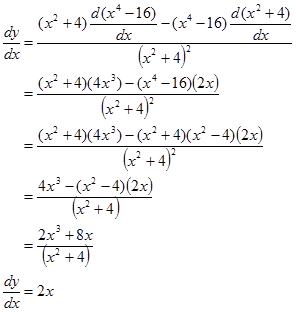

Bandingkan hasilnya dengan turunan fungsi $y=x^{8}-32x^{4}+256$.
7. Turunan fungsi rasional atau fungsi pembagian
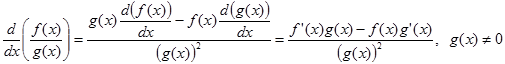
Contoh. Tentukan turunan $\frac{x^{4}-16}{x^{2}+4}$
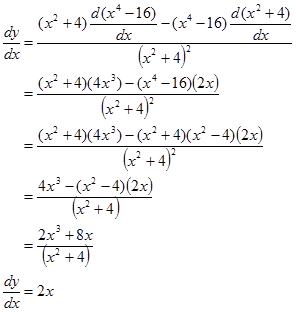
Bandingkan hasilnya dengan turunan fungsi $y=x^{2}-4$.


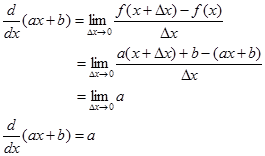

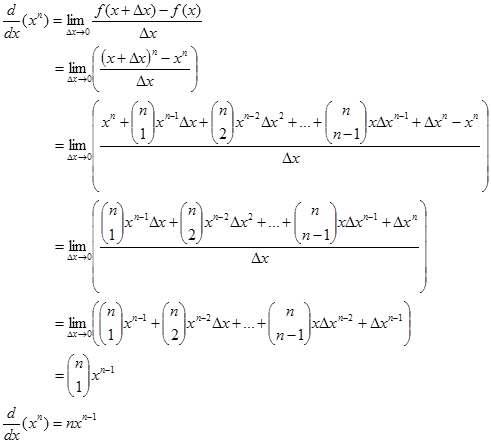

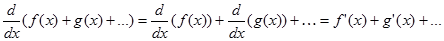













Tidak ada komentar:
Posting Komentar