Integral adalah bagian penting dari cabang matematika kalkulus yaitu suatu cabang matematika yang dibangun di atas dasar konsep limit. Secara garis besar integral ada dua macam yaitu integral tak tentu dan integral tentu.
Pada dasarnya, integral tak tentu adalah sebuah operasi pencarian anti turunan suatu fungsi. Sedangkan integral tentu awalnya adalah sebuah operasi pencarian luas daerah di bawah kurva, dan pengembangan lebih lanjut untuk mencari volume, titik berat, momen, dan lain-lain.
Di sini akan dibahas mengenai integral tak tentu, sifat-sifat, rumus-rumus integral tak tentu dan lebih dari 10 contoh soal integral tak tentu yang termasuk integral tak tentu fungsi aljabar.
Notasi integral tak tentu adalah "$\int$" (dibaca: integral) yang diikuti oleh $dx$, atau $dt$, atau $du$, atau lainnya tergantung dari variabel fungsi yang dicari integral tak tentu-nya.
1) $F(x)=x^5$→$F'(x)=5x^4$, maka $x^5$ adalah integral tak tentu dari $5x^4$. Ditulis $\int{5x^4}dx=x^5 + c$.
2) $F(t)=\frac{t^4}{4}$→$F'(t)=t^3$, maka $\frac{t^4}{4}$ adalah integral tak tentu dari $t^3$. Ditulis $\int{t^3}dt=\frac{t^4}{4} + c$
3) $F(u)=u^{-1}$→$F'(u)=-u^{-2}$, maka $u^{-1}$ adalah integral tak tentu dari $-u^{-2}$. Ditulis $-\int{u^{-2}}du=u^{-1} + c$
Integral tak tentu dari suatu fungsi tidak unik/ tunggal; sebagai contoh $x^5, x^5+5, x^5-5$, adalah integral tak tentu dari $f(x)=5x^4$ karena
$\frac{d}{dx}(x^5)=\frac{d}{dx}(x^5+5)=\frac{d}{dx}(x^5-5)=5x^4$
Semua integral tak tentu dari $5x^4$ kemudian dicakup dalam $x^5+C$, dengan C bilangan sembarang yang disebut konstanta pengintegralan.
Rumus yang lebih umum. Misalkan u adalah fungsi x yang dapat dideferensiasi, maka
Integral tak tentu
Jika $F(x)$ adalah sebuah fungsi yang turunannya $F'(x)=f(x)$, maka $F(x)$ disebut integral tak tentu (atau anti turunan) dari $f(x)$. Lihat turunan fungsi.Notasi integral tak tentu adalah "$\int$" (dibaca: integral) yang diikuti oleh $dx$, atau $dt$, atau $du$, atau lainnya tergantung dari variabel fungsi yang dicari integral tak tentu-nya.
Contoh integral tak tentu
1) $F(x)=x^5$→$F'(x)=5x^4$, maka $x^5$ adalah integral tak tentu dari $5x^4$. Ditulis $\int{5x^4}dx=x^5 + c$.
2) $F(t)=\frac{t^4}{4}$→$F'(t)=t^3$, maka $\frac{t^4}{4}$ adalah integral tak tentu dari $t^3$. Ditulis $\int{t^3}dt=\frac{t^4}{4} + c$
3) $F(u)=u^{-1}$→$F'(u)=-u^{-2}$, maka $u^{-1}$ adalah integral tak tentu dari $-u^{-2}$. Ditulis $-\int{u^{-2}}du=u^{-1} + c$
Integral tak tentu dari suatu fungsi tidak unik/ tunggal; sebagai contoh $x^5, x^5+5, x^5-5$, adalah integral tak tentu dari $f(x)=5x^4$ karena
$\frac{d}{dx}(x^5)=\frac{d}{dx}(x^5+5)=\frac{d}{dx}(x^5-5)=5x^4$
Semua integral tak tentu dari $5x^4$ kemudian dicakup dalam $x^5+C$, dengan C bilangan sembarang yang disebut konstanta pengintegralan.
Rumus integral tak tentu
Secara umum, Jika $F(x)$ adalah sebuah fungsi yang turunannya $F'(x)=f(x)$. Maka integral tak tent dari $f(x)$ dirumuskan denganini adalah rumus formal dan akan berubah sesuai dengan bentuk fungsi (mis. fungsi pangkat, fungsi trigonometri, fungsi rasional, dan sebagainya) yang dicari integralnya.
Sifat sifat integral tak tentu
Contoh
$\int{5x^4+6x^5}dx=x^5 + x^6+c$
$\int{t^3 - t^4}dt=\frac{t^4}{4} -\frac{t^5}{5}+ c$
Untuk sifat 5 dan 6 secara formal dapat diselesaikan dengan integral parsial, namun dalam kenyataannya itu tergantung situasi seperti pada contoh 2a dan 2d untuk perkalian dan 2b untuk pembagian dapat diselesaikan dengan menguasai rumus-rumus dasar integral tak tentu.
Integral fungsi pangkat
Rumus Integral fungsi pangkat yang lebih umum
Misalkan u adalah fungsi x yang dapat dideferensiasi, maka
Integral fungsi logaritma
dengan e adalah basis logaritma natural
Integral fungsi trigonometri
Misalkan u adalah fungsi x yang dapat dideferensiasi, maka
Integral fungsi rasional sederhana
Misalkan u adalah fungsi x yang dapat dideferensiasi, maka

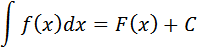

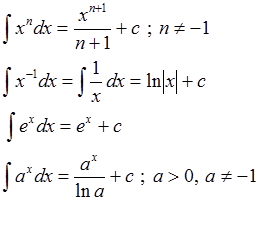

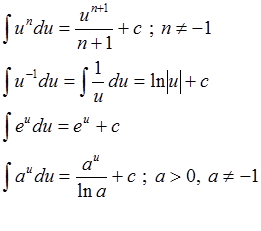
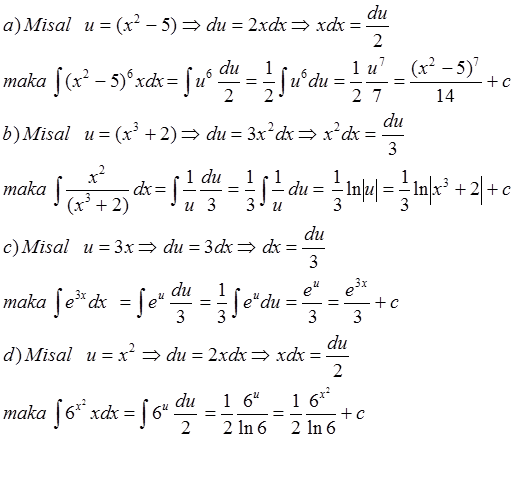
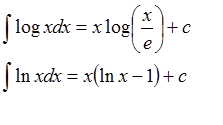
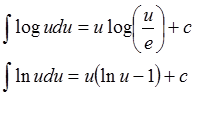
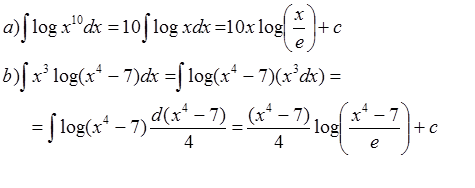

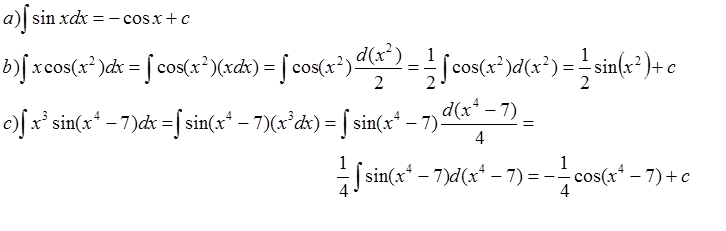
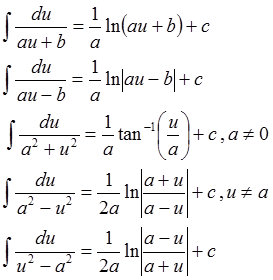
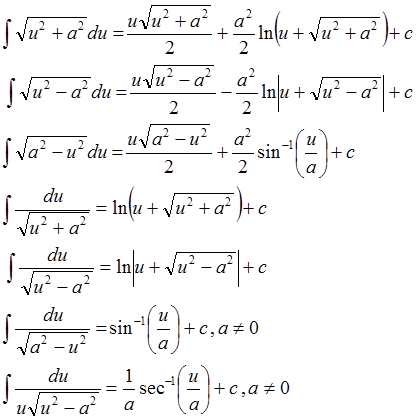










Tidak ada komentar:
Posting Komentar