Integral adalah bagian penting dari cabang matematika kalkulus yaitu suatu cabang matematika yang dibangun di atas dasar konsep limit. Secara garis besar integral ada dua macam yaitu integral tak tentu dan integral tentu. Pada dasarnya, integral tak tentu adalah sebuah operasi pencarian anti turunan suatu fungsi. Sedangkan integral tentu awalnya adalah sebuah operasi pencarian luas daerah di bawah kurva, dan pengembangan lebih lanjut untuk mencari volume, titik berat, momen, dan lain-lain.
Dalam postingan ini akan dibahas mengenai integral tentu.
Konsep dasar Integral Tentu
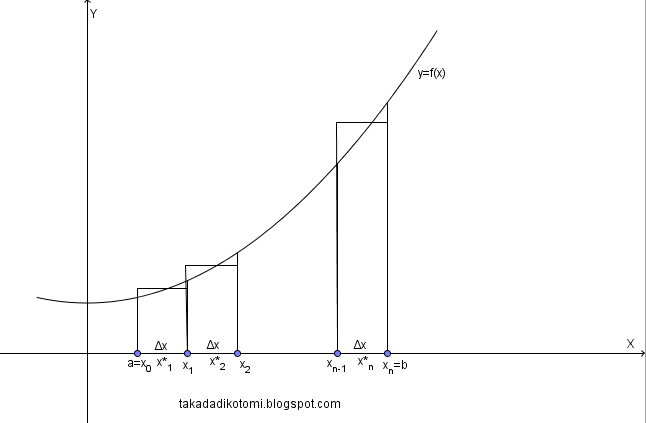
Misalkan kita ingin mengetahui luas di bawah kurva $y=f(x)$ yang kontinyu dalam selang $a≤x≤b$.
pertama, tentukan panjang selang yaitu $b–a$ kemudian bagilah selang tersebut menjadi $n$ subselang yang panjangnya sama sebesar $∆x=\frac{b-a}{n}$.
Kedua, misalkan $x_{0}=a, x_{1}=a+∆x, …, x_{n}=a+n∆x=b$, pilih titik-titik $x_{1}^*, x_{2}^*, …, x_{n}^*$ sehingga titik $x_{n}^*$ berada dalam subselang [$x_{n-1}, x_n$].
Catatan : $x_{n}^*$ ditentukan kemudian (lihat contoh soal integral tentu 1 dan 2).
Luas tiap subselang berbeda-beda dan dapat didekati dengan.
luas di bawah kurva $y=f(x)$ dari a sampai b dapat didekati dengan menjumlahkan semua luas subselang
Jika $n$ dibuat sangat besar maka banyak subselang akan mendekati tak terhingga dan luas tiap subselang akan akurat sehingga didapatkan luas di bawah kurva yang sebenarnya
Definisi integral tentu
integral tentu dari fungsi f(x) dalam selang a<=x<=b adalah
Teorema Dasar Kalkulus Integral
Jika $f(x)$ kontinyu dalam selang $a≤x≤b$ dan jika $F(x)$ adalah integral tak tentu dari $f(x)$, maka
Contoh 1. Kita akan menentukan luas di bawah garis y=x dari x=1 sampai x=5 dengan definisi integral tentu.
pertama, tentukan panjang selang yaitu $5–1=4$ kemudian bagilah selang tersebut menjadi $n$ subselang yang panjangnya sama sebesar $∆x=\frac{4}{n}$.
Kedua, misalkan $x_{0}=1, x_{1}=1+∆x, …, x_{n}=1+n∆x=5$, pilih titik-titik $x_{1}^*, x_{2}^*, …, x_{n}^*$ sehingga titik $x_{n}^*$ berada dalam subselang [$x_{n-1}, x_n$]. Dalam hal ini kita pilih
luas di bawah garis $y=x$ dari x=1 sampai x=5 adalah
Bandingkan hasilnya dengan
Sama khaaan ?
Contoh 2. Kita akan menentukan luas di bawah kurva $y=x^2$ dalam selang $2≤x≤5$, ambil $∆x=\frac{5-2}{n}=\frac{3}{n}$.
misalkan $x_{0}=2, x_{1}=2+∆x, …, x_{n}=2+n∆x=5$, kita pilih titik tengah
Sama khaaan ?
Perhatikan !. untuk menentukan luas di bawah kurva $y=x^2$ dengan definisi integral tentu kita memerlukan jumlah ke-n deret pangkat satu dan pangkat dua, jika pangkatnya semakin tinggi misalnya $y=x^{10}$ maka diperlukan jumlah ke-n deret pangkat satu, pangkat dua, pangkat tiga sampai pangkat sepuluh. Hal ini akan membuang banyak waktu. Oleh karena itu perhitungan integral tentu dengan definisi jarang dilakukan kecuali untuk penanaman konsep atau pembuktian.
Dan perhitungan akan lebih cepat dengan menggunakan Teorema Dasar Kalkulus Integral.
Sifat-sifat Integral Tentu
Jika $f(x)$ dan $g(x)$ kontinyu dalam selang integrasi $a≤x≤b$ , maka
Contoh 3. sifat integral tentu
Penerapan Integral Tentu
Integral Tentu banyak diterapkan tidak hanya pada bidang matematika itu sendiri tapi juga di fisika, kimia, aerodinamika, fisika nuklir, arsitektur dan sebagainya.
Luas Bidang
Penggunaan paling awal integral tentu adalah perhitungan luas bidang di bawah kurva atau garis seperti telah disebutkan di atas. Jika $f(x)$ kontinyu dan positif dalam selang $a≤x≤b$ maka luas kurva atau garis antara $x=a$ dan $x=b$ diberikan oleh
Contoh4. tentukan luas di bawah kurva $x^2-x$ dari $x=2$ sampai $x=5$
jawab:
Jika $f(x)$ negatif maka luas diberikan oleh
Contoh5. tentukan luas di bawah kurva $x-x^2$ dari $x=0$ sampai $x=5$
Pada selang 0<x<1 fungsi bernilai positif, sedangkan pada selang 1<x<=3 fungsi bernilai negatif padahal luas tak ada yng negatif maka
Bila $x=g(y)$ kontinyu dan positif dalam selang $a≤y≤b$ maka luas
kurva antara $y=a$ dan $y=b$ diberikan oleh
Bila $g(y)$ negatif maka luas diberikan oleh
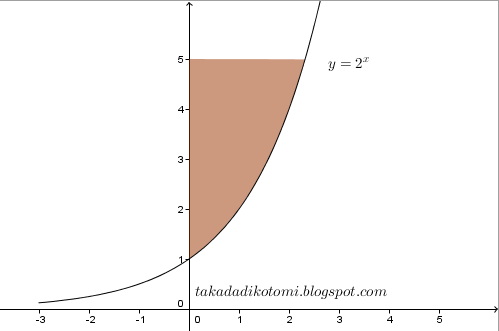
Contoh. Tentukan luas yang diberikan pada gambar berikut
Penyelesaian
Nyatakan x sebagai sebagai fungsi y.
Luas daerah adalah
Hasil akhir menggunakan kalkulator.
Lihat integral fungsi logaritma natural
Luas daerah antara dua kurva
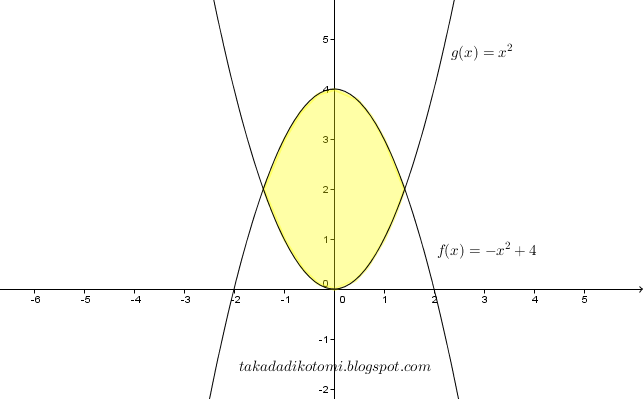
Contoh . tentukan luas daerah berwarna kuning muda pada gambar berikut
Penyelesaian
Tentukan dulu titik potong dua persamaan kuadrat tsb
Luas daerah adalah
Luas daerah pada dua luasan
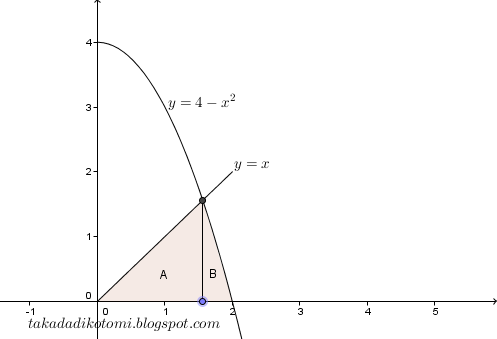
Contoh. Tentukan luas daerah berikut
Penyelesaian:
Pertama tentukan dulu titik potong kurva dan garis tersebut dengan bantuan persamaan kuadrat.
$x_2$ disini tidak diperlukan.Volum benda putar
Volum benda putar adalah volum benda yang terbentuk dari perputaran sebuah bidang datar di bawah kurva terhadap sumbu putar tertentu. Sumbu putar tertentu bisa saja sumbu-x, sumbu-y, garis $x=x_0$, atau garis $y=y_0$.
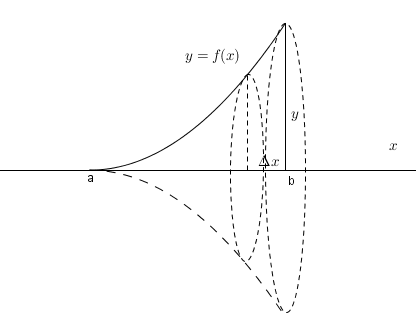
Sumbu putar sumbu-x
Perhatikan gambar
Luas penampang berbentuk lingkaran = $\pi y^2$,
Volum segmen berbentuk cakram $dV=\ pi y^2 \delta{x}$
Volum benda putar dari a sampai b
Sumbu putar sumbu-y
Perhatikan gambar
Luas penampang berbentuk lingkaran = $\pi x^2$,
Volum segmen berbentuk cakram $dV=\ pi x^2 \delta{y}$
Volum benda putar dari a sampai b
Contoh. Tentuan volum benda yang terjadi karena perputaran kurva $y=\sqrt{x}$
a) Seputar sumbu x dari x=0 sampai x=9.
b) Seputar sumbu y dari y=0 sampai y=3.
Penyelesaian
a) Volumnya adalah
b) ungkapkan x sebagai fungsi y -> $x=y^2$
Volumnya adalah
Panjang Busur
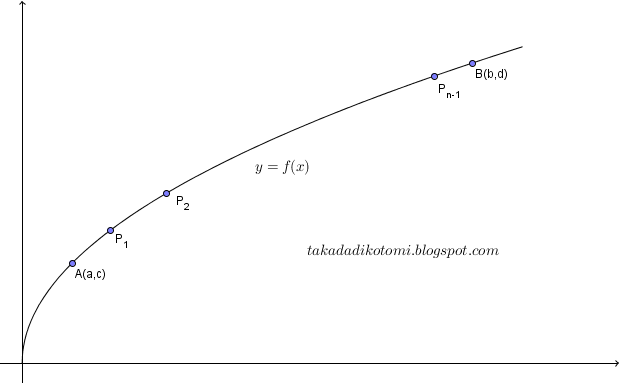
Panjang busur AB suatu kurva adalah limit penjumlahan panjang sekumpulan tali yang berderet $AP_{1}, P_{1}P_{2}, …, P_{n-1}B$ , yang menghubungkan semua titik pada busur itu. Jika banyak titik menuju nol sedemikian rupa sehingga panjang setiap tali menuju nol (bukan jadi nol), dan jika $A(a,c)$ dan $B(b,d)$ adalah dua titik pada kurva $y=f(x)$ dan turunannya kontinyu dalam selang $a<=x<=b$ maka panjang busur AB dinyatakan oleh
Dengan cara yang sama jika $A(a,c)$ dan $B(b,d)$ adalah dua titik pada kurva $x=g(y)$ dan turunannya kontinyu dalam selang $c<=x<=d$ maka panjang busur AB dinyatakan oleh
jika $A(u=u_{1})$ dan $B(u=u_{2})$ adalah dua titik pada kurva yang definisikan dengan persamaan parameter $x=f(u), y=g(u)$ dan syarat kontinuitas dipenuhi, maka panjang busur AB dinyatakan oleh
Contoh. Tentukan panjang busur kurva
a) $y=x^{\frac{3}{2}}$ dari x=2 sampai x=7
b) $y=x^{\frac{2}{3}}$ dari y=1 sampai x=5
Penyelesaan
a) Panjang busurnya adalah
b) Ungkapkan x sebagai fungsi y -> $x=y^{3/2}$
Panjang busurnya adalah

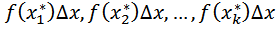
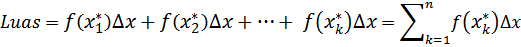
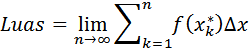

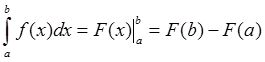
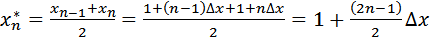
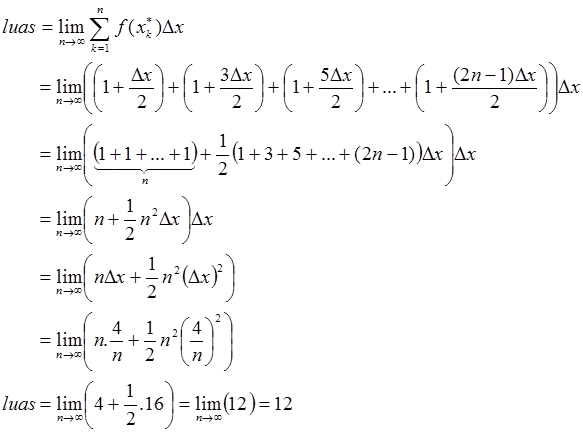
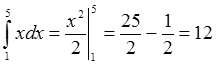
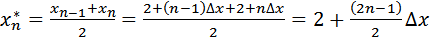
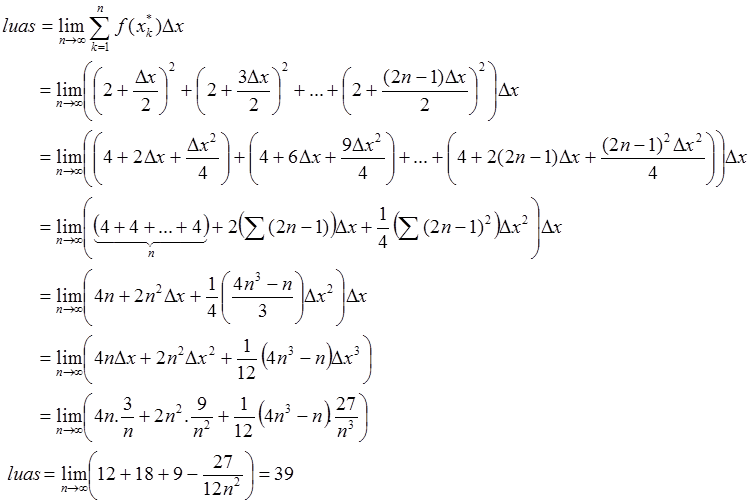
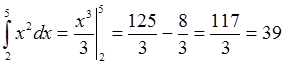

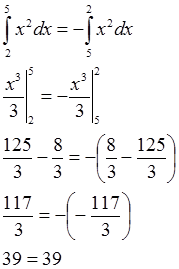
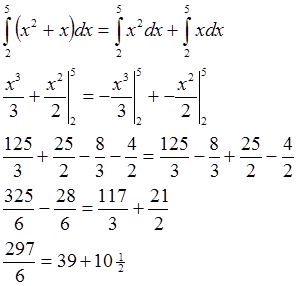

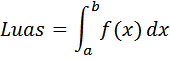
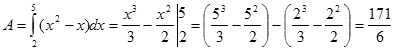
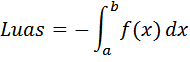
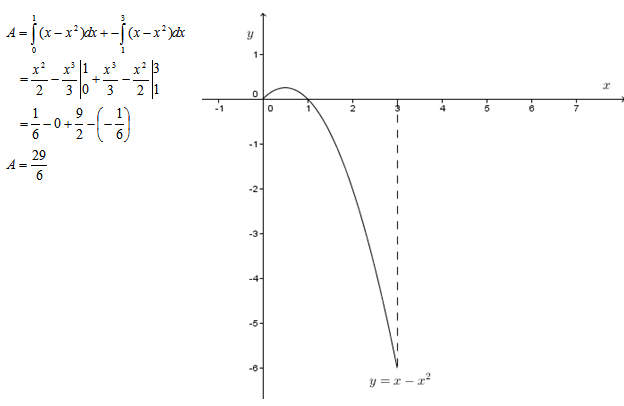
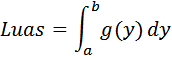
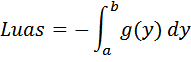
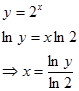
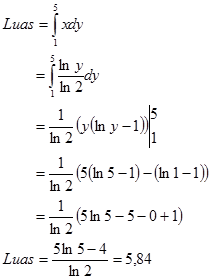
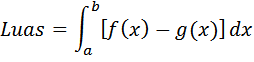
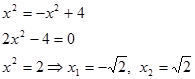
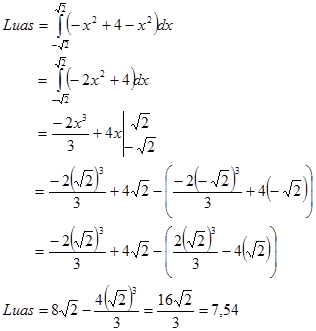
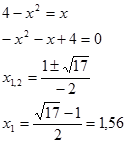
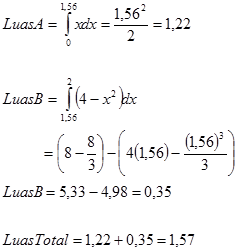
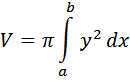



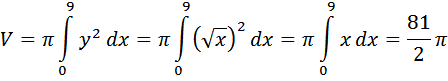
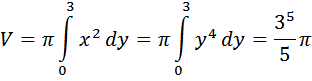
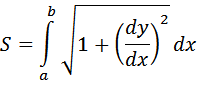
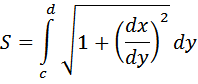
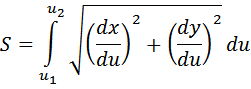
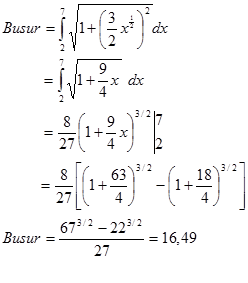
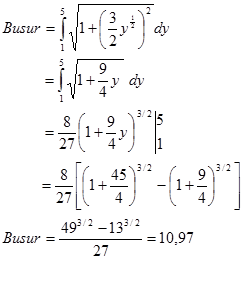









Tidak ada komentar:
Posting Komentar