content="vektor,
vektor bidang dan ruang,
definisi vektor,
contoh soal vektor dimensi 2,
pengertian vektor,
jenis jenis vektor,
pengertian vektor pada bidang dan ruang,
penjumlahan dan pengurangan vektor,
soal operasi vektor,
cara menghitung vektor" name=keywords
Vektor adalah besaran yang mempunyai nilai dan arah perpindahan misalnya kecepatan, gaya, percepatan, dll. Sedangkan besaran yang mempunyai nilai dan tidak mempunyai arah perpindahan disebut skalar misalnya massa, suhu, jumlah zat, dll.
Untuk memahami tentang vektor, lakukanlah kegiatan berikut.
1. Gambarlah sebuah ruas garis pada selembar kertas!
2. Berilah tanda panah pada ujung ruas garis tersebut ini!
3. Sebut titik pangkal ruas garis sebagai titik P dan titik ujungnya sebagai titik Q.
4. Ukurlah panjang ruas garis dengan menggunakan penggaris!
Ruas garis berarah yang kalian gambar pada kegiatan ini mewakili sebuah vektor. Panjang garis yang diukur menggunakan penggaris menunjukkan panjang vektor tersebut. Karena titik pangkal P dan titik ujung Q, maka vektor disebut sebagai vektor $\overrightarrow{PQ}$ .
Panjang vektor $\overrightarrow{PQ}$ ini dilambangkan dengan |$\overrightarrow{PQ}$|.
Selain cara di atas, sebuah vektor dapat pula ditulis menggunakan:
Seperti a, b, c, dan sebagainya. Misalnya, vektor $\overrightarrow{PQ}$ di bawah ditulis sebagai vektor a.
Penulisan vektor dengan tulisan tangan menggunakan lambang panah di atas huruf lebih sering digunakan, karena lebih mudah dituliskan dari pada yang dicetak tebal. Namun kebiasaan orang berbeda-beda, anda bebas memilih cara penulisan vektor yang disukai.
Dimana:
$i$: vektor satuan dalam bidang yang sejajar sumbu X yaitu i = (1,0)
$j$: vektor satuan dalam bidang yang sejajar sumbu Y yaitu j = (0,1)
Contoh. Tuliskan vektor $\vec{a}$ dengan titik pangkal A(2,3) dan titik ujung B(5,7) dalam bentuk vektor kolom, pasangan terurut dan vektor basis
jawab:
-vektor kolom
-Pasangan terurut
-Vektor basis
Dimana:
i: vektor satuan dalam ruang yang sejajar sumbu X yaitu i = (1,0,0)
j: vektor satuan dalam ruang yang sejajar sumbu Y yaitu j = (0,1,0)
k: vektor satuan dalam ruang yang sejajar sumbu Z yaitu k = (0,0,1)
Contoh. Tuliskan vektor a dengan titik pangkal A(2,3,6) dan titik ujung B(5,7,1) dalam bentuk vektor kolom, Pasangan terurut dan vektor basis
jawab:
-vektor kolom
-Pasangan terurut
-Vektor basis
vektor a mewakili ruas garis berarah dari titik pangkal $O(0,0)$ ke titik $A(a_{1}, a_{2})$. Oleh karena itu, vektor a ini dapat dituliskan dalam bentuk pasangan terurut $a=(a_{1}, a_{2})$. Adapun vektor b mewakili ruas garis berarah dari titik pangkal $O(0,0)$ ke titik $B(b_{1}, b_{2})$ . Vektor b dapat dituliskan sebagai $b=(b_{1}, b_{2})$. Karena vektor a dan b berawal dari titik pangkal $O(0,0)$, maka kedua vektor tersebut disebut vektor posisi. Sedangkan vektor c bukan vektor posisi. Namun, dalam kenyataannya setiap vektor dapat dinyatakan sebagai vektor posisi.
Secara umum untuk vektor $a(a_{1},a_{1})$, panjang Vektor dirumuskan
Contoh. Tentukan panjang vektor a dengan titik pangkal A(2,3) dan titik ujung B(5,7)
jawab:
vektor a adalah
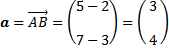
panjang vektor a adalah
Secara umum untuk vektor $a(a_{1}, a_{2},a_{3})$, panjang Vektor dirumuskan
Contoh. Tentukan panjang vektor dengan titik pangkal A(2,3,6) dan titik ujung B(5,7,1)
jawab:
vektor a adalah
panjang vektor a adalah
i = (1,0) adalah vektor satuan dalam bidang yang sejajar sumbu X.
j = (0,1) adalah vektor satuan dalam bidang yang sejajar sumbu Y.
i = (1,0,0) vektor satuan dalam bidang yang sejajar sumbu X.
j = (0,1,0) vektor satuan dalam bidang yang sejajar sumbu Y.
k = (0,0,1) vektor satuan dalam bidang yang sejajar sumbu Z.
Contoh . Tentukan vektor satuan dari 1) a = 6i+8j 2) b = 4i+4j+2k
Jawab:
1) panjang vektor a
2) panjang vektor b
Maka a + b = (a1 + b1, a2 + b2)
ka = (ka1, ka2)
Maka a + b = (a1 + b1, a2 + b2, a3 + b3)
ka = (k a1, k a2, k a3)
Berikut ini adalah sifat-sifat penjumlahan vektor berlaku pada vektor bidang dan vektor ruang.
Misalkan , a dan b adalah vektor-vektor, maka
1. Komutatif : a + b = b + a
2. Assosiatif : (a + b ) + c = a+(b+c)
3. Ada unsur identitas yaitu 0= (0, 0) atau 0 = (0, 0, 0) yang disebut vektor nol sehingga
a+ 0 = 0+ a = a
4. Ada vektor -a sehingga a +(-a) = 0
Untuk pengurangan
Pada penjumlahan vektor dengan aturan jajaran genjang, pangkal vektor a harus berimpit dengan pangkal vektor b.
Untuk pengurangan
Perhatikan gambar berikut
Vektor dan adalah dua vektor yang diketahui sedangkan tidak diketahui. Disisi lain titik C diketahui memagi ruas garis AB dengan perbandingan m:n yang diketahui. Dengan memanfaatkan perbandingan yang diketahui ini kita bisa menentukan vektor c yaitu sbb:
Rumus ini berlaku untuk vektor bidang dan ruang.
Contoh. Tentukan vektor c pada gambar di bawah
Jawab:
Dengan menukarkan a, b, c pada rumus 6.1 didapatkan titik koordinat C pada ruang:
Contoh. Diketahui titik A(2, 3, -1) dan B(7, -2, 9). Titik C membagi ruas garis AB dengan perbandingan 1:4. Carilah koordinat titik C
Jawab:
Jadi, koordinat titik C adalah (3, 2, 1).
Untuk vektor bidang , yang diperlukan hanya koordinat x dan y saja sehingga titik koordinat C pada bidang
Contoh. Diketahui titik P(2, 3, ) dan Q(7, 9). Titik R membagi ruas garis PQ dengan perbandingan 3:4. Carilah koordinat titik R
Jawab:
Jadi, koordinat titik R adalah (29/7, 39/7).
Dengan 𝞠 (teta) adalah sudut terkecil antara a dan b. Penerapan Rumus 8.1 (definisi) ini pada vektor basis dalam ruang dan atau bidang menghasilkan
Misalkan a = a₁i+a₂j membuat sudut 𝛼 dan 𝛽 masing-masing terhadap sumbu positif x, y. Dengan rumus 8.1 diperoleh
Didapat cosinus arah a yaitu
Misalkan a = a₁i + a₂j + a₃k membuat sudut 𝛼 , 𝛽 dan 𝛾 masing-masing terhadap sumbu positif x, y, z . Dengan rumus 8.1 diperoleh
Didapat cosinus arah a yaitu
Dan sudut antara dua vektor adalah
Contoh. Diketahui a = 4i + 4j + 2k dan a = 2i - 3j + 6k. Tentukan
1) Perkalian skalar a dan b
2) sudut antara a dan b
3) cosinus arah a dan b
Jawab:
1) Perkalian skalar a dan b
2) sudut antara a dan b
3) cosinus arah a dan b
cosinus arah a
cosinus arah b
1. jika 0 ≤ 𝞱 < 90 maka a.b > 0. Dalam hal ini 𝞱 berupa sudut lancip.
2. jika 90 < 𝞱 < 180 maka a.b < 0. Dalam hal ini 𝞱 berupa sudut tumpul.
3. jika 𝞱 = 90 maka a.b = 0. Dalam hal ini a dan b saling tegak lurus (ortogonal).
4. jika 𝞱 = 0 maka a.b = |a||b|. Dalam hal ini a dan b berimpit.
5. jika 𝞱 = 180 maka a.b = -|a||b|. Dalam hal ini a dan b berlawanan arah.
1. a.b = b.a
2. a.(b±c) = a.b ± a.c
3. m(a.b) = (ma).b = a.(mb) = (a.b)m , m sebuah skalar
4. a.a = |a|²
5. Jika a.b = 0 dimana a dan b bukan vektor nol maka a tegak lurus b.
Untuk proyeksi sebaliknya, misalkan vektor d adalah proyeksi vektor ortogonal dari vektor b pada arah vektor a. Dengan cara yang sama maka diperoleh
Proyeksi skalar ortogonal adalah panjang atau besar dari proyeksi vektor ortogonal. Proyeksi skalar ortogonal dari vektor a pada arah vektor b adalah |c| = |a|cos 𝛉. Dengan mengganti cos 𝛉 oleh rumus 7.7 didapat
Untuk proyeksi sebaliknya, misalkan vektor d adalah proyeksi skalar ortogonal dari vektor b pada arah vektor a. Dengan cara yang sama maka diperoleh
Contoh. Diketahui vektor a = 2i + j dan b = 3i + 4j adalah vektor-vektor basis di R2 . Carilah
1) Proyeksi vektor ortogonal dari vektor a pada arah vektor b
2) Proyeksi vektor ortogonal dari vektor b pada arah vektor a
3) Proyeksi skalar ortogonal dari vektor a pada arah vektor b
4) Proyeksi skalar ortogonal dari vektor b pada arah vektor a
Jawab:
Diketahui a.b = 10, |a| = √5, |b| = 5
1) Proyeksi vektor ortogonal dari vektor a pada arah vektor b
2) Proyeksi vektor ortogonal dari vektor b pada arah vektor a
3) Proyeksi skalar ortogonal dari vektor a pada arah vektor b
Hasil ini sama dengan menggunakan rumus panjang vektor untuk vekto c
4) Proyeksi skalar ortogonal dari vektor b pada arah vektor a
Hasil ini sama dengan menggunakan rumus panjang vektor untuk vekto d
Dengan 𝜃 adalah sudut terkecil antara a dan b, dan n adalah vektor normal satuan terhadap a dan b. Jika a dan b diganti vektor basis maka vektor normal satuan n adalah sbb:
Penerapan rumus 9.2 pada rumus 9.1 menghasilkan
Bentuk terakhir ini adalah penulisan hasil perkalian silang dalam bentuk determinan 3×3.
Lalu, apakah artinya rumus 9.5 secara geometri ?. Untuk itu perhatikan jajaran genjang yang dibentuk oleh vektor a dan b.
Luas jajaran genjang tersebut adalah
Dari ilustrasi ini dapat disimpulkan bahwa
Contoh. Diketahui a = 4i + 4j + 2k dan a = 2i - 3j + 6k. Tentukan
1) perkalian silang a dan b
2) luas paralelogram (jajaran genjang) dengan sisi a dan b adalah
Jawab:
1) perkalian silang a dan b
2) luas paralelogram (jajaran genjang) dengan sisi a dan b adalah
Contoh. Tentukan luas jajaran genjang berikut dengan metode perkalian vektor
Jawab:
Ambil a = 6i + 0j + 0k dan b = 0i + 4j + 0k , maka
luas jajaran genjang adalah 24 satuan.
2. a × (b ± c) = a × b ± a × c
3. m(a × b) = (ma)× b = a × (mb) = (a× b)m , m sebuah skalar
4. | a × b | = luas paralelogram (jajaran genjang) dengan sisi a dan b
5. Jika a × b = 0 dimana a dan b bukan vektor nol maka a sejajar b.

Vektor adalah besaran yang mempunyai nilai dan arah perpindahan misalnya kecepatan, gaya, percepatan, dll. Sedangkan besaran yang mempunyai nilai dan tidak mempunyai arah perpindahan disebut skalar misalnya massa, suhu, jumlah zat, dll.
Untuk memahami tentang vektor, lakukanlah kegiatan berikut.
1. Gambarlah sebuah ruas garis pada selembar kertas!
2. Berilah tanda panah pada ujung ruas garis tersebut ini!
3. Sebut titik pangkal ruas garis sebagai titik P dan titik ujungnya sebagai titik Q.
4. Ukurlah panjang ruas garis dengan menggunakan penggaris!
Ruas garis berarah yang kalian gambar pada kegiatan ini mewakili sebuah vektor. Panjang garis yang diukur menggunakan penggaris menunjukkan panjang vektor tersebut. Karena titik pangkal P dan titik ujung Q, maka vektor disebut sebagai vektor $\overrightarrow{PQ}$ .
Panjang vektor $\overrightarrow{PQ}$ ini dilambangkan dengan |$\overrightarrow{PQ}$|.
Selain cara di atas, sebuah vektor dapat pula ditulis menggunakan:
• huruf kecil yang dicetak tebal.
Seperti a, b, c, dan sebagainya. Misalnya, vektor $\overrightarrow{PQ}$ di bawah ditulis sebagai vektor a.
 |
| Gambar.1 |
• huruf kecil yang di atas huruf itu dibubuhi tanda panah.
Seperti $\vec{a}$, $\vec{b}$ , $\vec{c}$ dan sebagainya. Misalnya vektor dapat ditulis sebagai vektor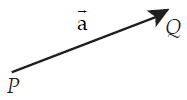 |
| Gambar.2 |
Penulisan vektor dengan tulisan tangan menggunakan lambang panah di atas huruf lebih sering digunakan, karena lebih mudah dituliskan dari pada yang dicetak tebal. Namun kebiasaan orang berbeda-beda, anda bebas memilih cara penulisan vektor yang disukai.
1 Cara Menuliskan Vektor
-Di R2 (dua dimensi)
Vektor bidang dengan titik pangkal $A(x_{1},y_{1})$ dan titik ujung $B(x_{2},y_{2})$ dinotasikan dengan $\overrightarrow{AB}$ dan dapat dituliskan dalam tiga cara yaitu: |
| Gambar.3 |
-vektor kolom
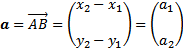 |
| Rumus 1.1 |
-Pasangan terurut
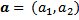 |
| Rumus 1.2 |
-Vektor basis
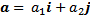 |
| Rumus 1.3 |
$i$: vektor satuan dalam bidang yang sejajar sumbu X yaitu i = (1,0)
$j$: vektor satuan dalam bidang yang sejajar sumbu Y yaitu j = (0,1)
Contoh. Tuliskan vektor $\vec{a}$ dengan titik pangkal A(2,3) dan titik ujung B(5,7) dalam bentuk vektor kolom, pasangan terurut dan vektor basis
jawab:
-vektor kolom
-Pasangan terurut
-Vektor basis
-Di R3 (tiga dimensi)
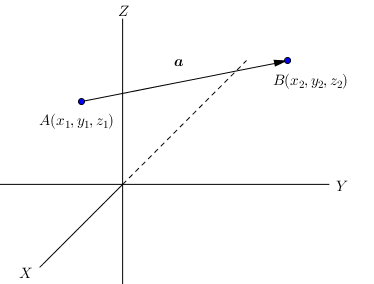
Vektor ruang dengan titik pangkal $A(x_{1},y_{1},z_{1})$ dan titik ujung $B(x_{2},y_{2},z_{2})$ dinotasikan dengan $\vec{a}=\overrightarrow{AB}$ dan dapat dituliskan dalam tiga cara yaitu: |
| Gambar.4 |
-vektor kolom
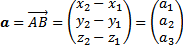 |
| Rumus 1.4 |
-Pasangan terurut
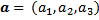 |
| Rumus 1.5 |
-Vektor basis
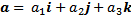 |
| Rumus 1.6 |
Dimana:
i: vektor satuan dalam ruang yang sejajar sumbu X yaitu i = (1,0,0)
j: vektor satuan dalam ruang yang sejajar sumbu Y yaitu j = (0,1,0)
k: vektor satuan dalam ruang yang sejajar sumbu Z yaitu k = (0,0,1)
Contoh. Tuliskan vektor a dengan titik pangkal A(2,3,6) dan titik ujung B(5,7,1) dalam bentuk vektor kolom, Pasangan terurut dan vektor basis
jawab:
-vektor kolom
-Pasangan terurut
-Vektor basis
Vektor Posisi
Sekarang, perhatikan sebarang titik $A(a_{1}, a_{2})$ dan titik $B(b_{1}, b_{2})$ pada koordinat Cartesius berikut.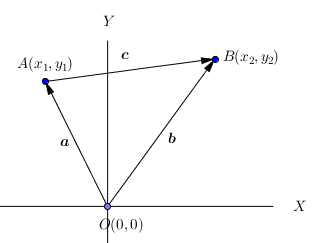 |
| Gambar.5 |
vektor a mewakili ruas garis berarah dari titik pangkal $O(0,0)$ ke titik $A(a_{1}, a_{2})$. Oleh karena itu, vektor a ini dapat dituliskan dalam bentuk pasangan terurut $a=(a_{1}, a_{2})$. Adapun vektor b mewakili ruas garis berarah dari titik pangkal $O(0,0)$ ke titik $B(b_{1}, b_{2})$ . Vektor b dapat dituliskan sebagai $b=(b_{1}, b_{2})$. Karena vektor a dan b berawal dari titik pangkal $O(0,0)$, maka kedua vektor tersebut disebut vektor posisi. Sedangkan vektor c bukan vektor posisi. Namun, dalam kenyataannya setiap vektor dapat dinyatakan sebagai vektor posisi.
2 Panjang Vektor
Panjang Vektor Dalam Bidang
Perhatikan gambar 5 di atas, dengan menggunakan rumus jarak, panjang vektor a dapat ditentukan dengan melihat keduanya berawal dari titik $A(x_{1},y_{1})$ dan titik ujung $B(x_{2},y_{2})$. Dengan menggunakan rumus jarak, panjang vektor a adalah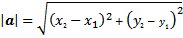 |
| Rumus 2.1 - Panjang Vektor Dalam bidang |
Secara umum untuk vektor $a(a_{1},a_{1})$, panjang Vektor dirumuskan
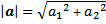 |
| Rumus 2.2 - Panjang Vektor Dalam bidang |
Contoh. Tentukan panjang vektor a dengan titik pangkal A(2,3) dan titik ujung B(5,7)
jawab:
vektor a adalah
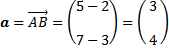
panjang vektor a adalah
Panjang Vektor Dalam Ruang
Perhatikan gambar 4 di atas, dengan menggunakan rumus jarak, panjang vektor a dapat ditentukan dengan melihat keduanya berawal dari titik $A(x_{1},y_{1},z_{1})$ dan titik ujung $B(x_{2},y_{2},z_{2})$. Dengan menggunakan rumus jarak, panjang vektor a adalah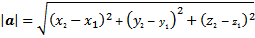 |
| Rumus 2.3 - Panjang Vektor Dalam Ruang |
Secara umum untuk vektor $a(a_{1}, a_{2},a_{3})$, panjang Vektor dirumuskan
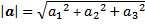 |
| Rumus 2.4 - Panjang Vektor Dalam Ruang |
Contoh. Tentukan panjang vektor dengan titik pangkal A(2,3,6) dan titik ujung B(5,7,1)
jawab:
vektor a adalah
panjang vektor a adalah
3 Vektor Satuan
Vektor satuan adalah vektor yang panjangnya satu satuan, biasanya dilambangkan dengan e. Cara membuat vektor satuan dari vektor a adalah dengan membagi vektor a oleh panjangnya sendiri, secara matematis dirumuskan dengan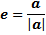 |
| Rumus 3.1 - vektor satuan |
Vektor satuan dari vektor basis yang saling tegak lurus
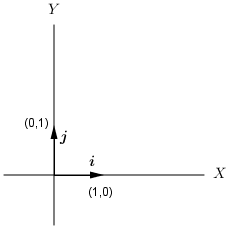
- Pada vektor bidang
 |
| Gambar.7 |
i = (1,0) adalah vektor satuan dalam bidang yang sejajar sumbu X.
j = (0,1) adalah vektor satuan dalam bidang yang sejajar sumbu Y.
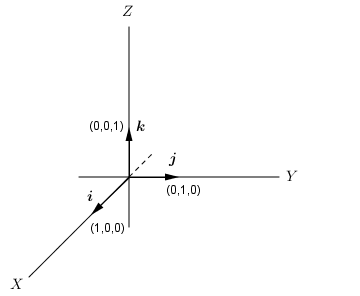
- Pada vektor ruang
 |
| Gambar.8 |
i = (1,0,0) vektor satuan dalam bidang yang sejajar sumbu X.
j = (0,1,0) vektor satuan dalam bidang yang sejajar sumbu Y.
k = (0,0,1) vektor satuan dalam bidang yang sejajar sumbu Z.
Contoh . Tentukan vektor satuan dari 1) a = 6i+8j 2) b = 4i+4j+2k
Jawab:
1) panjang vektor a
vektor satuannya
2) panjang vektor b
vektor satuannya
4 Operasi vektor Secara analitik (aljabar)
Pada vektor bidang
Misalkan a = (a1, a2), b = (b1, b2), k bilangan realMaka a + b = (a1 + b1, a2 + b2)
ka = (ka1, ka2)
pada vektor ruang
Misalkan a = (a1, a2, a3), b = (b1, b2, b3), k bilangan realMaka a + b = (a1 + b1, a2 + b2, a3 + b3)
ka = (k a1, k a2, k a3)
Berikut ini adalah sifat-sifat penjumlahan vektor berlaku pada vektor bidang dan vektor ruang.
Misalkan , a dan b adalah vektor-vektor, maka
1. Komutatif : a + b = b + a
2. Assosiatif : (a + b ) + c = a+(b+c)
3. Ada unsur identitas yaitu 0= (0, 0) atau 0 = (0, 0, 0) yang disebut vektor nol sehingga
a+ 0 = 0+ a = a
4. Ada vektor -a sehingga a +(-a) = 0
5 Operasi vektor Secara Geometri
Aturan segitiga
Pada penjumlahan vektor dengan aturan segitiga , ujung vektor a harus berimpit dengan pangkal vektor b.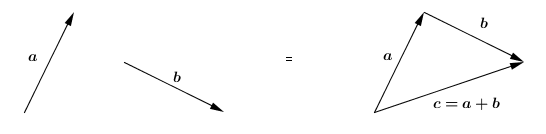 |
| Gambar.9 |
Untuk pengurangan
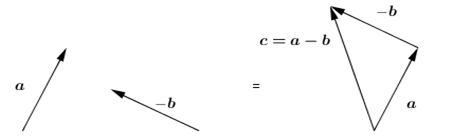 |
| Gambar.10 |
Aturan jajaran genjang
Pada penjumlahan vektor dengan aturan jajaran genjang, pangkal vektor a harus berimpit dengan pangkal vektor b.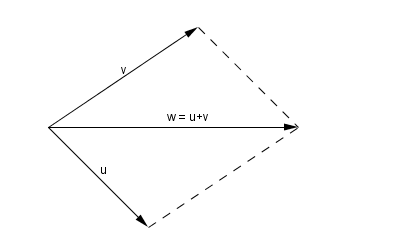 |
| Gambar.11 |
Untuk pengurangan
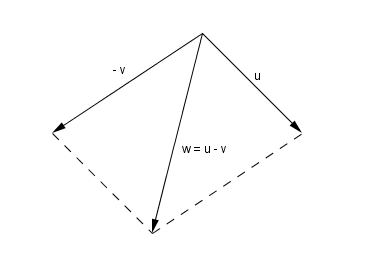 |
| Gambar.12 |
Aturan polygon
Aturan polygon digunakan untuk penjumlahan lebih dari dua vektor. Ujung vektor pertama harus berimpit dengan pangkal vektor kedua, ujung vektor kedua harus berimpit dengan pangkal vektor ketiga, dan seterusnya.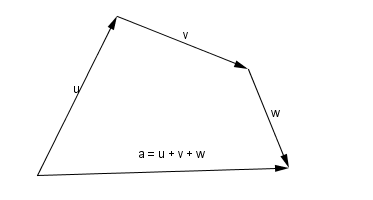 |
| Gambar.13 |
6 Pembagian ruas garis dalam bentuk vektor
Perhatikan gambar berikut
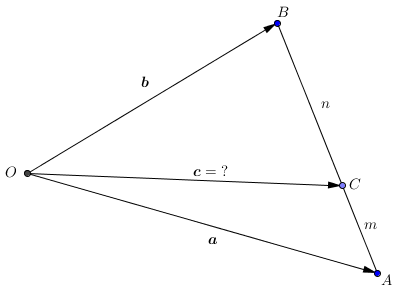 |
| Gambar.14 |
Vektor dan adalah dua vektor yang diketahui sedangkan tidak diketahui. Disisi lain titik C diketahui memagi ruas garis AB dengan perbandingan m:n yang diketahui. Dengan memanfaatkan perbandingan yang diketahui ini kita bisa menentukan vektor c yaitu sbb:
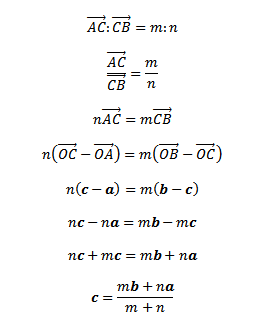 |
| Rumus 6.1 - Pembagian ruas garis bentuk vektor |
Contoh. Tentukan vektor c pada gambar di bawah
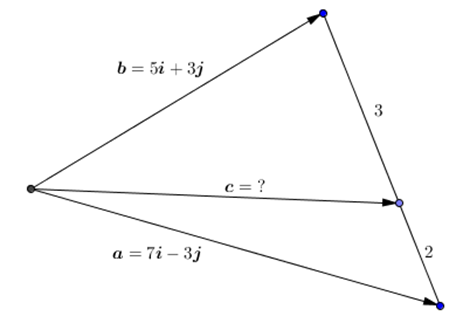 |
| gambar.15 |
Pembagian ruas garis dalam bentuk koordinat
Rumus pembagian ruas garis dapat pula dinyatakan dalam bentuk koordinat. Untuk vektor ruang, misalkan vektor posisi titik A, B, C berturut-turut adalahDengan menukarkan a, b, c pada rumus 6.1 didapatkan titik koordinat C pada ruang:
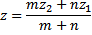 |
| Rumus 6.2 - Pembagian ruas garis bentuk koordinat R3 |
Contoh. Diketahui titik A(2, 3, -1) dan B(7, -2, 9). Titik C membagi ruas garis AB dengan perbandingan 1:4. Carilah koordinat titik C
Jawab:
Jadi, koordinat titik C adalah (3, 2, 1).
Untuk vektor bidang , yang diperlukan hanya koordinat x dan y saja sehingga titik koordinat C pada bidang
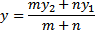 |
| Rumus 6.3 - Pembagian ruas garis bentuk koordinat R2 |
Contoh. Diketahui titik P(2, 3, ) dan Q(7, 9). Titik R membagi ruas garis PQ dengan perbandingan 3:4. Carilah koordinat titik R
Jawab:
Jadi, koordinat titik R adalah (29/7, 39/7).
7 Perkalian Titik (dot product)
Perkalian titik atau dot product sering disebut juga perkalian skalar karena menghasilkan sebuah skalar, bukan vektor. Misalkan a dan b adalah vektor-vektor bidang atau ruang, maka perkalian titik antara a dan b didefinisikan dengan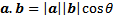 |
| Rumus 7.1 |
Dengan 𝞠 (teta) adalah sudut terkecil antara a dan b. Penerapan Rumus 8.1 (definisi) ini pada vektor basis dalam ruang dan atau bidang menghasilkan
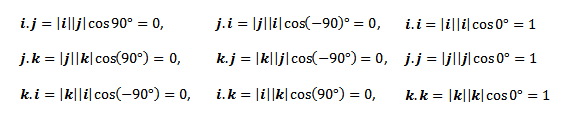 |
| Rumus 7.2 |
Perkalian Titik dalam bentuk komponen pada Vektor Bidang
Misalkan a = a₁i+a₂j dan b = b₁i+b₂j adalah vektor-vektor bidang, maka dengan mengunakan rumus 8.2 perkalian titik antara a dan b dalam bentuk komponen adalah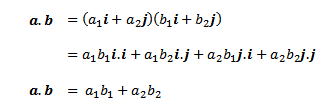 |
| Rumus 7.3 |
Cosinus arah vektor bidang
Misalkan a = a₁i+a₂j membuat sudut 𝛼 dan 𝛽 masing-masing terhadap sumbu positif x, y. Dengan rumus 8.1 diperolehDidapat cosinus arah a yaitu
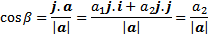 |
| Rumus 7.4 |
Perkalian Titik dalam bentuk komponen pada Vektor Ruang
Misalkan a = a₁i + a₂j + a₃k dan b = b₁i + b₂j + b₃k adalah vektor-vektor ruang, maka perkalian titik antara a dan b maka dengan mengunakan rumus 7.2 perkalian titik antara a dan b dalam bentuk komponen adalah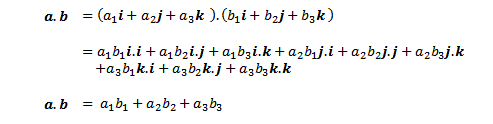 |
| Rumus 7.5 |
Cosinus arah vektor ruang
Misalkan a = a₁i + a₂j + a₃k membuat sudut 𝛼 , 𝛽 dan 𝛾 masing-masing terhadap sumbu positif x, y, z . Dengan rumus 8.1 diperolehDidapat cosinus arah a yaitu
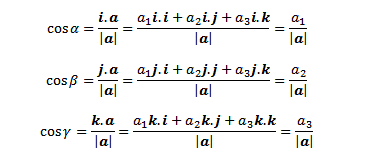 |
| Rumus 7.6 |
Sudut antara dua vektor
Dari definisi ( rumus 7.1) didapatkan Sudut antara dua vektor bidang atau ruang sbb: |
| Rumus 7.7 |
 |
| Rumus 7.8 - sudut antara dua vektor |
Contoh. Diketahui a = 4i + 4j + 2k dan a = 2i - 3j + 6k. Tentukan
1) Perkalian skalar a dan b
2) sudut antara a dan b
3) cosinus arah a dan b
Jawab:
1) Perkalian skalar a dan b
2) sudut antara a dan b
3) cosinus arah a dan b
cosinus arah a
cosinus arah b
Tanda-tanda perkalian titik
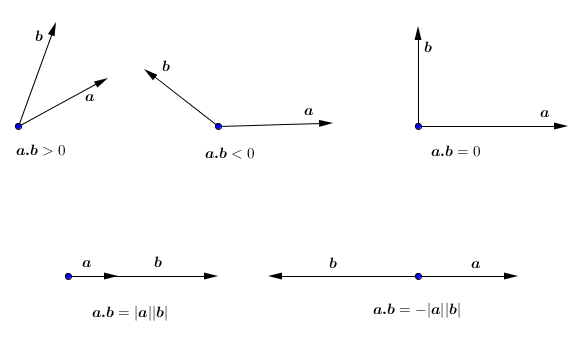 |
| Gambar.16 |
2. jika 90 < 𝞱 < 180 maka a.b < 0. Dalam hal ini 𝞱 berupa sudut tumpul.
3. jika 𝞱 = 90 maka a.b = 0. Dalam hal ini a dan b saling tegak lurus (ortogonal).
4. jika 𝞱 = 0 maka a.b = |a||b|. Dalam hal ini a dan b berimpit.
5. jika 𝞱 = 180 maka a.b = -|a||b|. Dalam hal ini a dan b berlawanan arah.
Sifat-sifat perkalian titik
Sifat-sifat berikut berlaku untuk vektor bidang dan ruang.1. a.b = b.a
2. a.(b±c) = a.b ± a.c
3. m(a.b) = (ma).b = a.(mb) = (a.b)m , m sebuah skalar
4. a.a = |a|²
5. Jika a.b = 0 dimana a dan b bukan vektor nol maka a tegak lurus b.
8 Proyeksi Ortogonal suatu vektor pada vektor yang lain
Vektor c adalah proyeksi atau bayangan vektor a pada vektor b (gambar menyusul). Dengan pengandaian sumber cahaya tegak lurus vektor b.Proyeksi Vektor Ortogonal
Proyeksi vektor ortogonal dari vektor a pada arah vektor b adalah c = |c|e dengan e adalah vektor satuan dari vektor c. karena vektor c searah vektor b maka vektor satuan dari c sama dengan vektor satuan dari b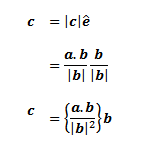 |
| Rumus 8.1 |
Untuk proyeksi sebaliknya, misalkan vektor d adalah proyeksi vektor ortogonal dari vektor b pada arah vektor a. Dengan cara yang sama maka diperoleh
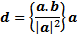 |
| Rumus 8.2 |
Proyeksi Skalar Ortogonal
Proyeksi skalar ortogonal adalah panjang atau besar dari proyeksi vektor ortogonal. Proyeksi skalar ortogonal dari vektor a pada arah vektor b adalah |c| = |a|cos 𝛉. Dengan mengganti cos 𝛉 oleh rumus 7.7 didapat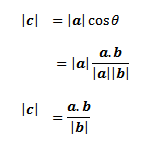 |
| Rumus 8.3 |
Untuk proyeksi sebaliknya, misalkan vektor d adalah proyeksi skalar ortogonal dari vektor b pada arah vektor a. Dengan cara yang sama maka diperoleh
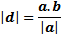 |
| Rumus 8.4 |
Contoh. Diketahui vektor a = 2i + j dan b = 3i + 4j adalah vektor-vektor basis di R2 . Carilah
1) Proyeksi vektor ortogonal dari vektor a pada arah vektor b
2) Proyeksi vektor ortogonal dari vektor b pada arah vektor a
3) Proyeksi skalar ortogonal dari vektor a pada arah vektor b
4) Proyeksi skalar ortogonal dari vektor b pada arah vektor a
Jawab:
Diketahui a.b = 10, |a| = √5, |b| = 5
1) Proyeksi vektor ortogonal dari vektor a pada arah vektor b
2) Proyeksi vektor ortogonal dari vektor b pada arah vektor a
3) Proyeksi skalar ortogonal dari vektor a pada arah vektor b
Hasil ini sama dengan menggunakan rumus panjang vektor untuk vekto c
4) Proyeksi skalar ortogonal dari vektor b pada arah vektor a
Hasil ini sama dengan menggunakan rumus panjang vektor untuk vekto d
9 Perkalian Silang (cross product)
Perkalian silang atau cross product disebut juga perkalian vektor karena hasilnya adalah sebuah vektor, bukan skalar. Perkalian silang berlaku pada vektor ruang namun dalam penerapannya bisa juga diterapkan pada vektor bidang. Perkalian silang antara a dan b didefinisikan dengan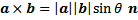 |
| Rumus 9.1 |
Dengan 𝜃 adalah sudut terkecil antara a dan b, dan n adalah vektor normal satuan terhadap a dan b. Jika a dan b diganti vektor basis maka vektor normal satuan n adalah sbb:
 |
| Gambar.17 (kurang tanda siku-siku) |
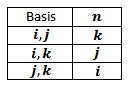 |
| Rumus 9.2 |
Penerapan rumus 9.2 pada rumus 9.1 menghasilkan
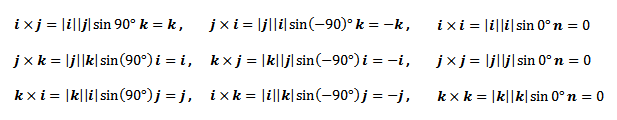 |
| Rumus 9.3 |
Perkaliang silang dalam Bentuk Komponen
Sekarang misalkan a dan b adalah vektor-vektor ruang, dengan menggunakan rumus 9.3 maka perkalian silang antara a dan b adalah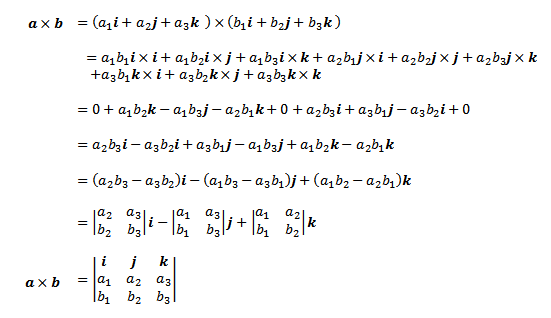 |
| Rumus 9.4 |
Bentuk terakhir ini adalah penulisan hasil perkalian silang dalam bentuk determinan 3×3.
Besar perkalian silang
Besar suatu perkalian silang ditentukan sbb: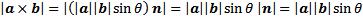 |
| Rumus 9.5 |
Lalu, apakah artinya rumus 9.5 secara geometri ?. Untuk itu perhatikan jajaran genjang yang dibentuk oleh vektor a dan b.
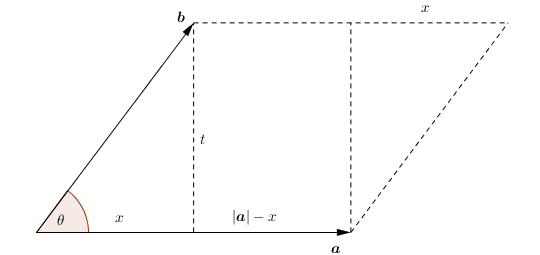 |
| Gambar 18 |
Luas jajaran genjang tersebut adalah
Dari ilustrasi ini dapat disimpulkan bahwa
Contoh. Diketahui a = 4i + 4j + 2k dan a = 2i - 3j + 6k. Tentukan
1) perkalian silang a dan b
2) luas paralelogram (jajaran genjang) dengan sisi a dan b adalah
Jawab:
1) perkalian silang a dan b
2) luas paralelogram (jajaran genjang) dengan sisi a dan b adalah
Contoh. Tentukan luas jajaran genjang berikut dengan metode perkalian vektor
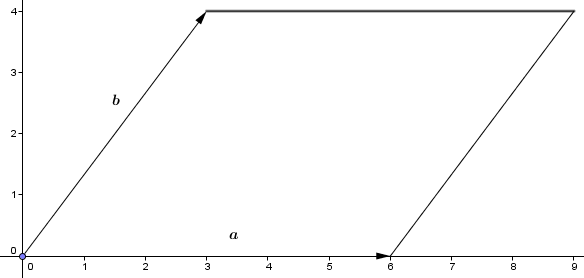 |
| Gambar 19 |
Jawab:
Ambil a = 6i + 0j + 0k dan b = 0i + 4j + 0k , maka
luas jajaran genjang adalah 24 satuan.
Sifat-sifat perkalian silang
1. a × b = - b × a2. a × (b ± c) = a × b ± a × c
3. m(a × b) = (ma)× b = a × (mb) = (a× b)m , m sebuah skalar
4. | a × b | = luas paralelogram (jajaran genjang) dengan sisi a dan b
5. Jika a × b = 0 dimana a dan b bukan vektor nol maka a sejajar b.

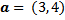
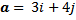
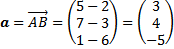
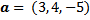
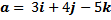
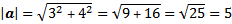
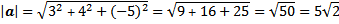
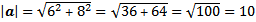
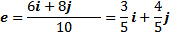
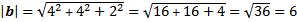
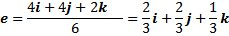
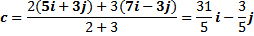
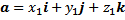
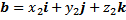
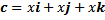
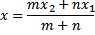
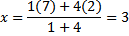
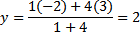
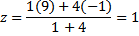
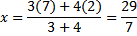
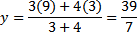


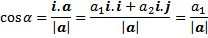

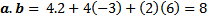
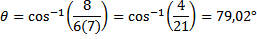
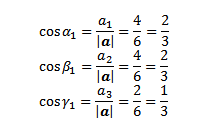
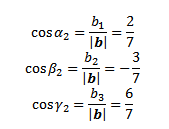
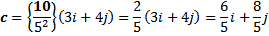

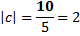
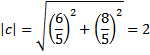
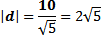
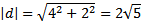
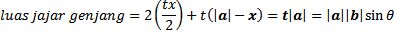
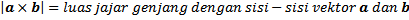
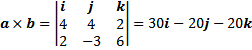
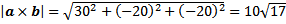












Tidak ada komentar:
Posting Komentar