Determinan matriks adalah nilai penentu pada matriks persegi. Sedangkan pada matriks non persegi tidak ada determinan. Determinan matriks $A$ dinotasikan dengan $det(A)$ atau $|A|$. Determinan sebuah matriks dapat dijabarkan berdasarkan ekspansi baris atau kolom dimana semua ekspansi tersebut menghasilkan nilai yang sama. Secara formal determinan matriks $A$ ordo $n×n$ yang dijabarkan berdasarkan ekspansi baris pertama dirumuskan dengan
Dimana $M_{1j}$ menyatakan determinan matriks minor yaitu matriks yang berordo lebih rendah dari $n×n$ setelah dibuang baris ke-1 kolom ke-j. Untuk matriks $1×1$ didefinisikan determinannya sama dengan elemennya.
Determinan Matriks 2×2
Misalkan A adalah matriks ordo 2×2 berbentuk
maka
Dalam bentuk yang lebih mudah, misalkan A adalah matriks ordo 2x2 berbentuk
Maka $det(A)=ad-bc $
Contoh 1. Tentukan determinan matriks-matriks berikut
Jawab
Contoh 2. Tentukan nilai x, y dan z dari determinan-determinan berikut
Jawab
Penerapan Determinan 2×2 pada SPLDV
Determinan 2x2 digunakan dalam metode Cramer untuk menyelesaikan sistem persamaan linear dua variabel (SPLDV). Misalkan SPLDV dalam variabel x dan y.
Nilai x dan y ditentukan dengan rumus
Contoh. Tentukan himpunan penyelesaian
Jawab:
Jadi himpunan penyelesaian adalah {(4,7)}.
Determinan Matriks 3×3
Misalkan $A$ adalah matriks ordo $3x3$ berbentuk
maka
Contoh 3. Tentukan determinan matriks berikut dengan ekspansi determinan
Jawab:
Aturan Sarrus
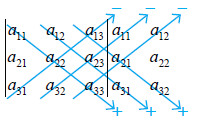
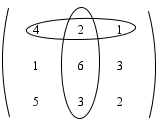
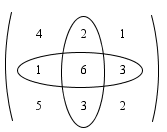
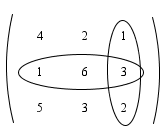
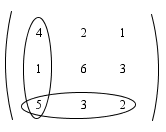
Ada suatu cara yang mudah untuk menghitung determinan 3x3 yang disebut aturan Sarrus. Perhatikan bagan aturan Sarrus berikut
Tanda panah ke kanan bawah menyatakan perkalian elemen-elemen bertanda positif, sedangkan tanda panah ke kanan atas menyatakan perkalian elemen-elemen bertanda negatif.
Yang mana hasilnya sama dengan yang dihasilkan rumus determinan dengan sedikit perbedaan urutan elemen. Namun itu bukan masalah karena perkalian bersifat komutatif.
Contoh 4. Tentukan determinan matriks berikut dengan aturan Sarrus
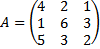
Jawab:
Penerapan Determinan 3x3 pada SPLTV
Determinan 3x3 digunakan dalam metode Cramer untuk menyelesaikan sistem persamaan linear tiga variabel (SPLTV). Misalkan SPLTV dalam variabel x, y dan z.
Nilai x, y dan z ditentukan dengan rumus
Contoh. Tentukan himpunan penyelesaian
Jawab:
Jadi himpunan penyelesaian adalah {(10, 6, 2)}.
Sifat-sifat Determinan
1. $det (A B) = det(A) det (B)$
Contoh. Diketahui
Maka
2. $det (A + B) ≠det(A) + det(B)$
Contoh. Diketahui
Maka
3. $A_{n×n } ⇒det(k A) = k^{n}det(A)$
Contoh. Diketahui
Maka
4. $det (A^t) = det(A)$
Contoh. Diketahui
Maka
5. $det ( A^{-1} ) =\frac{1}{det(A)}$
Contoh. Diketahui
Maka
Dimana $Adj(A)$ adalah matriks adjoin yang dihasilkan dari transpos matriks kofaktor $kof(A)$. Jika $det(A) = 0$ maka $A$ tidak punya invers dan $A$ disebut matriks singular.
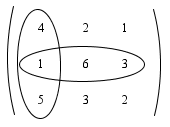
Dimana $M_{ij}$ menyatakan determinan matriks minor yaitu matriks yang berordo lebih rendah dari $n×n$ dari matriks A setelah dibuang baris ke-i kolom ke-j. Berikut adalah kontruksi matriks kofaktor
Maka matriks kofaktor dari A adalah
Adjoin A diperoleh dengan mentrasposkan matriks kofaktor
Sehingga invers matriks ordo 2x2 dapat dituliskan sebagai
Dalam bentuk yang lebih mudah, misalkan A adalah matriks ordo 2x2 berbentuk
Maka
Contoh 5. Tentukan invers matriks-matriks berikut
Jawab:
c) Matriks C tidak punya invers karena det(C)=0
Dapat diselesaikan dengan penerapan invers matriks 2x2 setelah sistem persamaan tersebut diubah kedalam bentuk persamaan matriks
Solusi persamaan matriks ini diberikan oleh
Contoh 6. Tentukan penyelesaian sistem persamaan linear dua variabel (SPLDV) berikut
Jawab:
Ubah dahulu sistem persamaan linear dua variabel ke dalam bentuk persamaan matriks
Jadi, penyelesaian adalah {(5,7)}
Maka matriks kofaktor dari A adalah
Adjoin A diperoleh dengan mentrasposkan matriks kofaktor
Sehingga invers matriks ordo 3x3 dapat dituliskan sebagai
Contoh 7. Tentukan invers matriks berikut dengan metode kofaktor
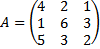
Jawab:
Dari contoh 3 diketahui det(A)=11
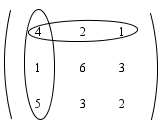
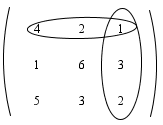
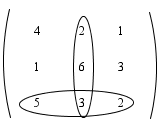
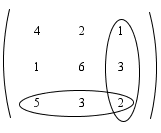
Menentukan kofaktor-kofaktor
Matriks kofaktor
Adjoin A adalah
Maka invers A adalah
Baca juga: soal-dan-pembahasan-matriks
Dapat diselesaikan dengan penerapan invers matriks 3x3 setelah sistem persamaan tersebut diubah kedalam bentuk persamaan matriks
Solusi persamaan matriks ini diberikan oleh
Contoh 8. Tentukan penyelesaian sistem persamaan linear tiga variabel (SPLTV) berikut
Jawab:
Ubah dahulu sistem persamaan linear tiga variabel ke dalam bentuk persamaan matriks
Jadi, HP={(2, 1, 9)}
Secara umum, ordo matriks yang dihasilkan dari persamaan matriks $AX=B$ akan sama dengan ordo matriks $B$ dan penyelesaiannya dirumuskan dengan
Untuk lebih jelasnya perhatikan contoh berikut.
Contoh. Carilah matriks X, Y dan Z dari persamaan-persamaan berikut
Pembahasan
1. Matriks X berordo 2x2
2. Matriks Y berordo 3x3
3. Matriks Z berordo 2x3
Contoh. Diketahui
Maka
2. $(A^{-1})^{-1} = A$
Contoh. Diketahui
Maka
3. $(A B )^{-1} = B^{-1}A^{-1}$
Contoh. Diketahui
Maka
Maka
3. $A_{n×n } ⇒det(k A) = k^{n}det(A)$
Contoh. Diketahui
Maka
4. $det (A^t) = det(A)$
Contoh. Diketahui
Maka
5. $det ( A^{-1} ) =\frac{1}{det(A)}$
Contoh. Diketahui
Maka
Invers Matriks
Invers dari matriks $A$ ditulis $A^{-1}$ dan didefinisikan sebagai berikutDimana $Adj(A)$ adalah matriks adjoin yang dihasilkan dari transpos matriks kofaktor $kof(A)$. Jika $det(A) = 0$ maka $A$ tidak punya invers dan $A$ disebut matriks singular.
Matriks kofaktor
Matriks kofaktor adalah matriks yang semua elemennya dihasilkan dari rumus kofaktorDimana $M_{ij}$ menyatakan determinan matriks minor yaitu matriks yang berordo lebih rendah dari $n×n$ dari matriks A setelah dibuang baris ke-i kolom ke-j. Berikut adalah kontruksi matriks kofaktor
Invers matriks 2x2
Misalkan A adalah matriks ordo 2x2 berbentukAdjoin A diperoleh dengan mentrasposkan matriks kofaktor
Sehingga invers matriks ordo 2x2 dapat dituliskan sebagai
Dalam bentuk yang lebih mudah, misalkan A adalah matriks ordo 2x2 berbentuk
Maka
Contoh 5. Tentukan invers matriks-matriks berikut
Jawab:
c) Matriks C tidak punya invers karena det(C)=0
Penerapan Invers Matriks 2×2 pada Penyelesaian SPLDV
Sebuah sistem persamaan dua variabel (SPLDV) yang berbentukDapat diselesaikan dengan penerapan invers matriks 2x2 setelah sistem persamaan tersebut diubah kedalam bentuk persamaan matriks
Solusi persamaan matriks ini diberikan oleh
Contoh 6. Tentukan penyelesaian sistem persamaan linear dua variabel (SPLDV) berikut
Jawab:
Ubah dahulu sistem persamaan linear dua variabel ke dalam bentuk persamaan matriks
Jadi, penyelesaian adalah {(5,7)}
Invers matriks 3x3
Misalkan A adalah matriks ordo 3x3 berbentukMaka matriks kofaktor dari A adalah
Adjoin A diperoleh dengan mentrasposkan matriks kofaktor
Sehingga invers matriks ordo 3x3 dapat dituliskan sebagai
Contoh 7. Tentukan invers matriks berikut dengan metode kofaktor
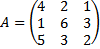
Jawab:
Dari contoh 3 diketahui det(A)=11
Menentukan kofaktor-kofaktor
Matriks kofaktor
Adjoin A adalah
Maka invers A adalah
Baca juga: soal-dan-pembahasan-matriks
Penerapan Invers matriks 3x3 pada Penyelesaian SPLTV
Sebuah sistem persamaan tiga variabel (SPLTV) yang berbentukDapat diselesaikan dengan penerapan invers matriks 3x3 setelah sistem persamaan tersebut diubah kedalam bentuk persamaan matriks
Solusi persamaan matriks ini diberikan oleh
Contoh 8. Tentukan penyelesaian sistem persamaan linear tiga variabel (SPLTV) berikut
Jawab:
Ubah dahulu sistem persamaan linear tiga variabel ke dalam bentuk persamaan matriks
Jadi, HP={(2, 1, 9)}
Penyelesaian Persamaan Matriks AX=B
Suatu persamaan matriks bentuk $AX=B$ cara penyelesaiannya telah disinggung pada penerapan invers matriks 2x2 dan 3x3 pada penyelesaian SPLDV dan SPLTV. Hasilnya berupa matriks kolom yang berisi dua elemen atau tiga elemen.Secara umum, ordo matriks yang dihasilkan dari persamaan matriks $AX=B$ akan sama dengan ordo matriks $B$ dan penyelesaiannya dirumuskan dengan
Untuk lebih jelasnya perhatikan contoh berikut.
Contoh. Carilah matriks X, Y dan Z dari persamaan-persamaan berikut
1.
2.
3.
Pembahasan
1. Matriks X berordo 2x2
2. Matriks Y berordo 3x3
3. Matriks Z berordo 2x3
Sifat-sifat Invers Matriks
1. $A = B^{-1}⇔B = A^{-1}$Contoh. Diketahui
Maka
2. $(A^{-1})^{-1} = A$
Contoh. Diketahui
Maka
3. $(A B )^{-1} = B^{-1}A^{-1}$
Contoh. Diketahui
Maka


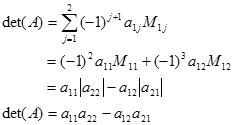
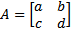
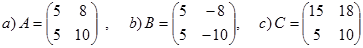
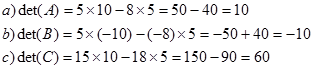
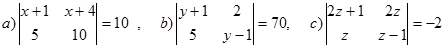
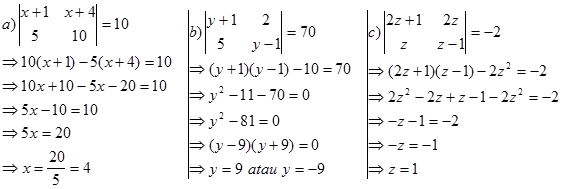
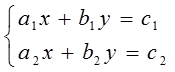
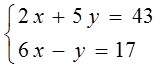

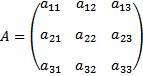
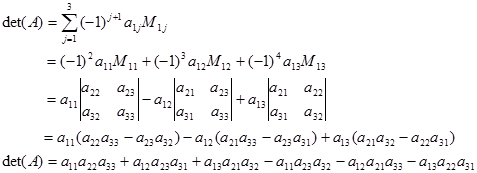
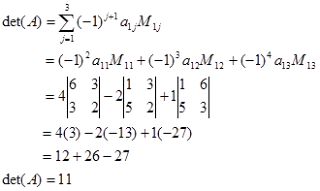


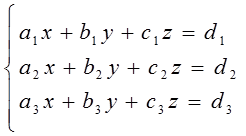
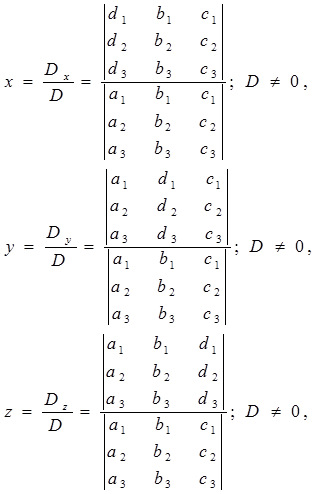
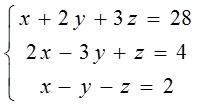
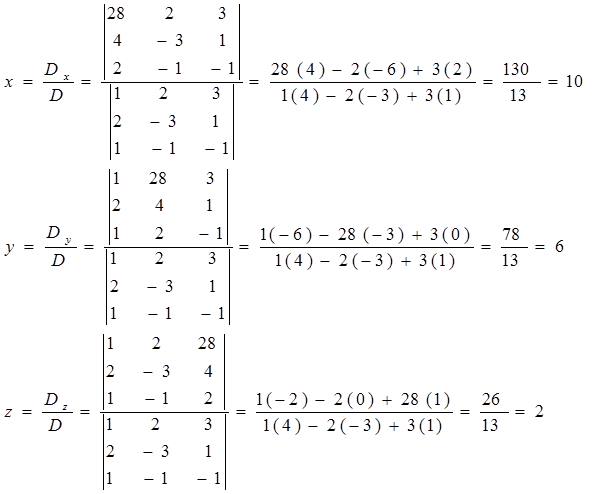
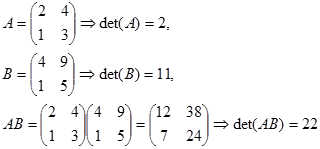
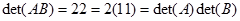

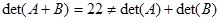
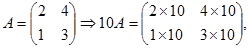
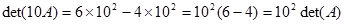
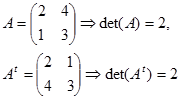
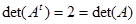
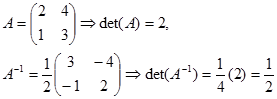

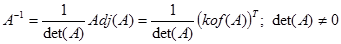
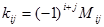
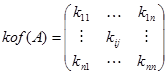
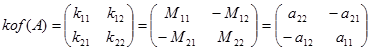
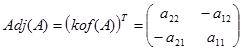
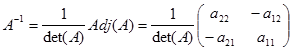
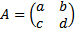
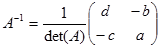

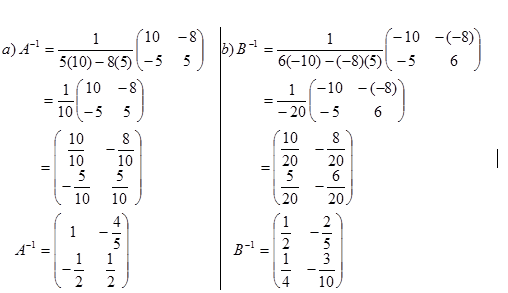
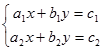
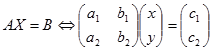
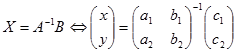
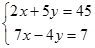



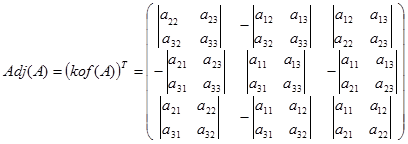
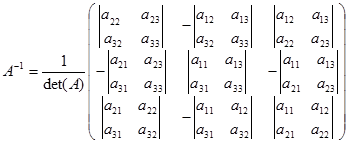
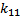

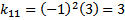
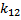
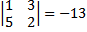
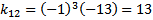
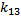
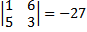
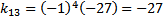
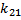
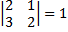
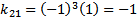
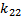
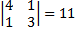
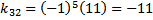

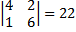
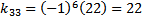



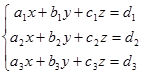
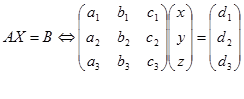
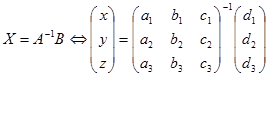
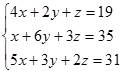
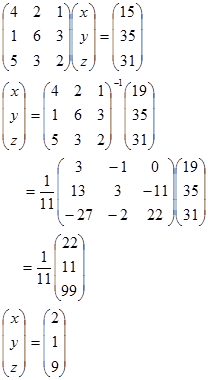
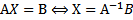
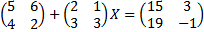
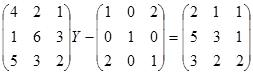

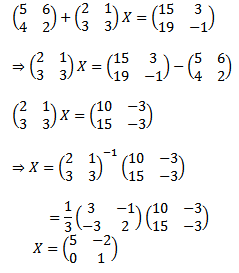
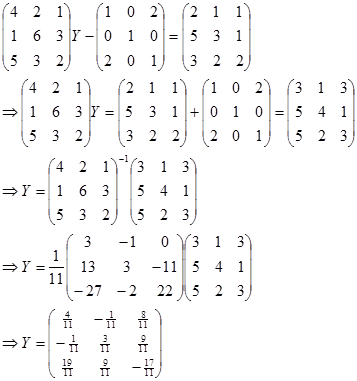
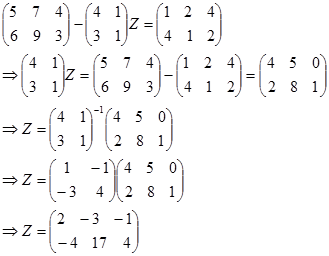
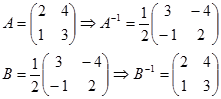

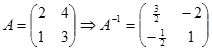
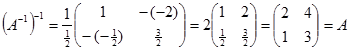
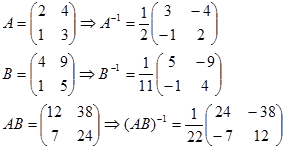
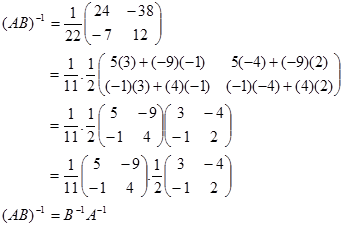









Tidak ada komentar:
Posting Komentar