Fungsi aljabar adalah fungsi yang paling sering ditemui dalam permasalahan matematika yang meliputi fungsi rasional, linear, kuadrat, kubik dan seterusnya.
Suatu fungsi aljabar (bidang) adalah fungsi yang persamaannya dapat ditulis sebagai
Dengan $u_{n}(x)$ adalah suatu polinomial dalam $x$.
Contoh. fungsi kuadrat $y = x^{2} – 10x+25$. Dari fungsi ini maka didapat $n=2, a=0, b=0, c=1, d=-1, e=10, f=-25$, dan $u_{3}(x)=u_{4}(x)=…=u_{n}(x)=0$.
Turunan fungsi aljabar dapat diperoleh dengan menerapkan definisi turunan fungsi pada fungsi-fungsi aljabar. Suatu fungsi aljabar (begitu juga fungsi transenden misalnya fungsi trigonometri) dapat diturunkan di $x = a $ jika fungsi itu mempunyai turunan di titik tersebut. Suatu fungsi aljabar dapat diturunkan pada suatu selang jika fungsi itu mempunyai turunan di setiap titik pada selang tersebut.
Bukti
Contoh
Bukti
Contoh. $y=4x+5⇒\frac{dy}{dx}=4$
Bukti
contoh
Contoh
Dapat disimpulkan bahwa operator d/dx bersifat linear pada penjumlahan fungsi
Contoh
Dapat disimpulkan bahwa operator d/dx bersifat linear pada pengurangan fungsi
Contoh
Bandingkan hasilnya dengan turunan fungsi $y=x^{4}-16$.
Turunan perkalian fungsi dapat diperluas untuk perkalian lebih dari dua fungsi misalnya tiga fungsi dengan menerapkan aturan perkalian dua fungsi secara berulang. Misalkan $f=f(x), g=g(x)$, dan $h=h(x)$.
Contoh
Bandingkan hasilnya dengan turunan fungsi $y=x^{8}-32x^{4}+256$.
Contoh. Tentukan turunan $\frac{x^{4}-16}{x^{2}+4}$
Bandingkan hasilnya dengan turunan fungsi $y=x^{2}-4$.
Contoh. Cari $\frac{dy}{dx}$ jika diketahui $x=\sqrt{y}$
Contoh. Tentukan dy/dx jika $x=2t-2, y=t^2$
jawab
Penerapan aturan rantai pada fungsi pangkat
Misalkan u adalah suatu fungsi x, maka
Contoh. Tentukan turunan dari $y=(x^{3}+2x)^{10}$
Demikian pula jika $y=f(u), u=g(v) $dan $v=h(x)$, maka
Contoh. Tentukan turunan dari $y=\sqrt[3]{(x^{3}+2x)^{10}}$
Jawab:
Contoh
Meskipun turunan derajat-n diperoleh dengan menurunkan fungsi sebanyak derajat n yang diperlukan yang mana kita harus menurunkan fungsi sebanyak n kali. Dalam kenyataanya ada beberapa fungsi yang turunan derajat-n-nya dapat diperoleh secara langsung seperti pada fungsi pangkat.
Dari sini kita punya dua versi turunan derajat ke-n yaitu:
Versi ini lebih cocok untuk fungsi yang berpangkat bulat positif.
Contoh
namun bentuk faktorialnya akan sedikit membingungkan jika n >= m+1 bernilai negatif. Seperti contoh berikut
Padahal jika diperiksa dengan aturan faktorial yang mengalikan bilangan-bilangan berikutnya dengan selisih 1, maka turunan ke-3-nya bernilai nol begitu juga seterusnya sebagai mana berikut
Dari sini kita bisa membuat batasan yaitu
Contoh
Versi ini lebih cocok Jika fungsi pangkat mempunyai pangkat real tidak bulat atau bulat negatif atau pecahan (positif dan negatif), dimana turunan ke-n-nya tidak pernah bernilai nol, artinya turunan ke-n-nya selalu ada untuk n berapapun juga.
Contoh.
Perhatikan, menggunakan versi permutasi juga hasilnya sama namun langkah penyelesaian jadi lebih lama karena harus menjabarkan dulu faktorial real positif tidak bulat atau faktorial negatif atau pecahan yang mungkin agak membingungkan. Seperti berikut
Begitu juga dengan faktorial pecahan atau faktorial real positif tidak bulat seperti pada contoh di atas, operasi perkalian tidak akan berhenti karena tidak ada bilangan pecahan negatif terkecil yang ditemui.
Suatu fungsi aljabar (bidang) adalah fungsi yang persamaannya dapat ditulis sebagai
Dengan $u_{n}(x)$ adalah suatu polinomial dalam $x$.
Contoh. fungsi kuadrat $y = x^{2} – 10x+25$. Dari fungsi ini maka didapat $n=2, a=0, b=0, c=1, d=-1, e=10, f=-25$, dan $u_{3}(x)=u_{4}(x)=…=u_{n}(x)=0$.
Turunan fungsi aljabar dapat diperoleh dengan menerapkan definisi turunan fungsi pada fungsi-fungsi aljabar. Suatu fungsi aljabar (begitu juga fungsi transenden misalnya fungsi trigonometri) dapat diturunkan di $x = a $ jika fungsi itu mempunyai turunan di titik tersebut. Suatu fungsi aljabar dapat diturunkan pada suatu selang jika fungsi itu mempunyai turunan di setiap titik pada selang tersebut.
1. Turunan fungsi konstan
Misalkan $y =f(x) = c$, dengan $c$ sebuah konstanta sembarang makaBukti
Contoh
2. Turunan fungsi linear
Misalkan $y =f(x) = ax+b$, dengan a tidak nol dan b sebuah konstanta sembarang makaBukti
Contoh. $y=4x+5⇒\frac{dy}{dx}=4$
3. Turunan fungsi pangkat
Misalkan $y =f(x) = x^n$, dengan n bilangan real, makaBukti
contoh
4. Turunan penjumlahan fungsi
Contoh
Dapat disimpulkan bahwa operator d/dx bersifat linear pada penjumlahan fungsi
5. Turunan pengurangan fungsi
Contoh
Dapat disimpulkan bahwa operator d/dx bersifat linear pada pengurangan fungsi
6. Turunan perkalian (dua) fungsi
Contoh
Bandingkan hasilnya dengan turunan fungsi $y=x^{4}-16$.
Turunan perkalian fungsi dapat diperluas untuk perkalian lebih dari dua fungsi misalnya tiga fungsi dengan menerapkan aturan perkalian dua fungsi secara berulang. Misalkan $f=f(x), g=g(x)$, dan $h=h(x)$.
Contoh
Bandingkan hasilnya dengan turunan fungsi $y=x^{8}-32x^{4}+256$.
7. Turunan fungsi rasional atau fungsi pembagian
Contoh. Tentukan turunan $\frac{x^{4}-16}{x^{2}+4}$
Bandingkan hasilnya dengan turunan fungsi $y=x^{2}-4$.
8. Turunan fungsi invers
Misalkan $y=f(x)$ dan $x = g(y)$ maka $\frac{dy}{dx}$ dan $\frac{dx}{dy}$ dihubungkan denganContoh. Cari $\frac{dy}{dx}$ jika diketahui $x=\sqrt{y}$
9. Turunan fungsi parametrik
Jika $x=f(t)$ dan $y=g(t)$ makaContoh. Tentukan dy/dx jika $x=2t-2, y=t^2$
jawab
10. Aturan rantai / Turunan fungsi suatu fungsi
Jika $y=f(u)$ dimana $u =g(x)$, makaPenerapan aturan rantai pada fungsi pangkat
Misalkan u adalah suatu fungsi x, maka
Contoh. Tentukan turunan dari $y=(x^{3}+2x)^{10}$
Demikian pula jika $y=f(u), u=g(v) $dan $v=h(x)$, maka
Contoh. Tentukan turunan dari $y=\sqrt[3]{(x^{3}+2x)^{10}}$
Jawab:
11. Turunan lebih tinggi
Turunan lebih tinggi disebut juga turunan derajat-n adalah turunan-turunan berikutnya dari turunan pertama suatu fungsi. Turunan lebih tinggi diperoleh dengan menurunkan fungsi sebanyak derajat yang diperlukan, misalnya diperlukan turunan kedua maka fungsi diturunkan dua kali, diperlukan turunan ketiga maka fungsi diturunkan tiga kali dan seterusnya. Ada beberapa notasi untuk turunan derajat-n yang sering digunakan untuk turunan kedua, ketiga, keempat dan seterusnya sebagai berikut.|
|
|
|
Meskipun turunan derajat-n diperoleh dengan menurunkan fungsi sebanyak derajat n yang diperlukan yang mana kita harus menurunkan fungsi sebanyak n kali. Dalam kenyataanya ada beberapa fungsi yang turunan derajat-n-nya dapat diperoleh secara langsung seperti pada fungsi pangkat.
Dari sini kita punya dua versi turunan derajat ke-n yaitu:
a) Versi permutasi atau faktorial
Versi ini lebih cocok untuk fungsi yang berpangkat bulat positif.
Contoh
namun bentuk faktorialnya akan sedikit membingungkan jika n >= m+1 bernilai negatif. Seperti contoh berikut
Padahal jika diperiksa dengan aturan faktorial yang mengalikan bilangan-bilangan berikutnya dengan selisih 1, maka turunan ke-3-nya bernilai nol begitu juga seterusnya sebagai mana berikut
Dari sini kita bisa membuat batasan yaitu
Contoh
b) Versi perkalian
Versi ini lebih cocok Jika fungsi pangkat mempunyai pangkat real tidak bulat atau bulat negatif atau pecahan (positif dan negatif), dimana turunan ke-n-nya tidak pernah bernilai nol, artinya turunan ke-n-nya selalu ada untuk n berapapun juga.
Contoh.
Perhatikan, menggunakan versi permutasi juga hasilnya sama namun langkah penyelesaian jadi lebih lama karena harus menjabarkan dulu faktorial real positif tidak bulat atau faktorial negatif atau pecahan yang mungkin agak membingungkan. Seperti berikut
Out Of Topic
Dari sini kita bisa mengambil pelajaran bahwa faktorial negatif berbeda dengan faktorial positif. Pada faktorial positif, berapapun besarnya bilangan, operasi perkalian akan berhenti pada bilangan bulat positif terkecil yaitu 1. Sedangkan pada faktorial negatif, berapapun kecilnya bilangan, operasi perkalian tidak akan berhenti karena tidak ada bilangan bulat negatif terkecil.Begitu juga dengan faktorial pecahan atau faktorial real positif tidak bulat seperti pada contoh di atas, operasi perkalian tidak akan berhenti karena tidak ada bilangan pecahan negatif terkecil yang ditemui.

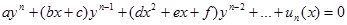

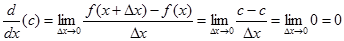
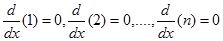
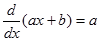
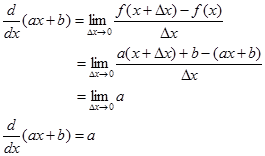

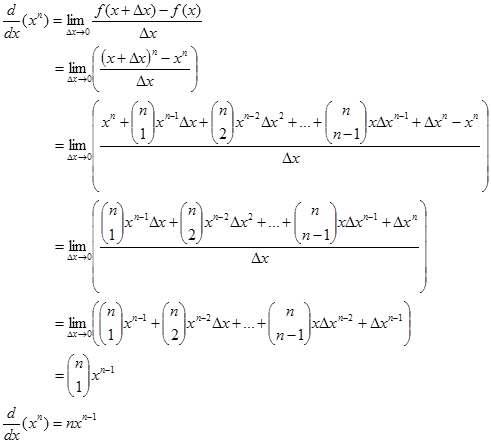

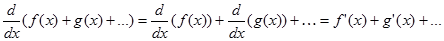
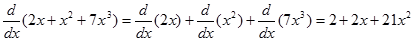
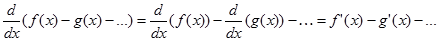
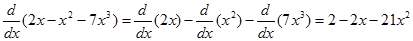
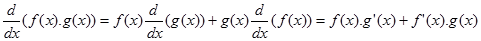
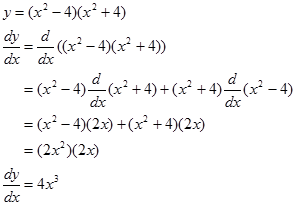
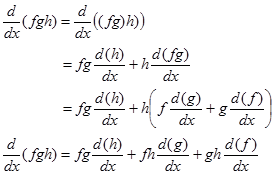

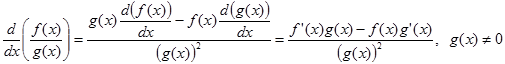
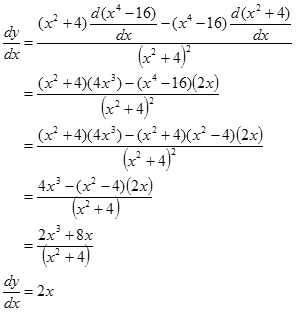
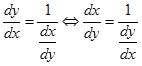
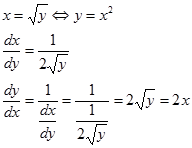
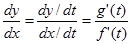

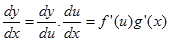
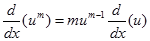
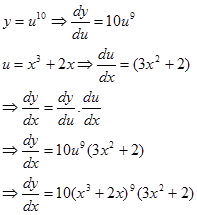
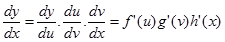

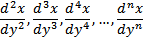
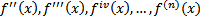
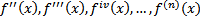
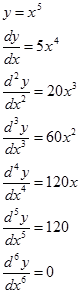
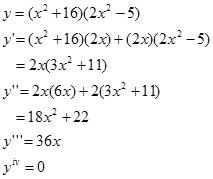
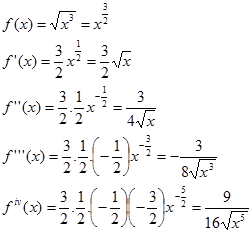
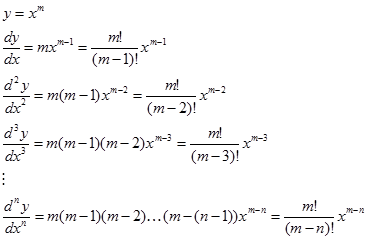
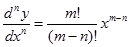
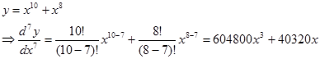
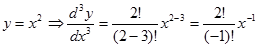
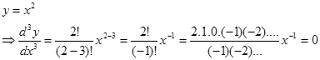
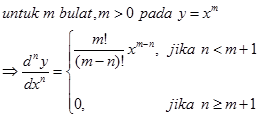
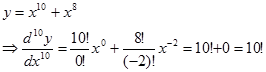
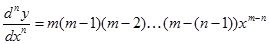
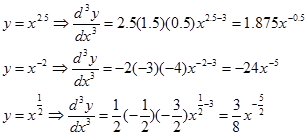
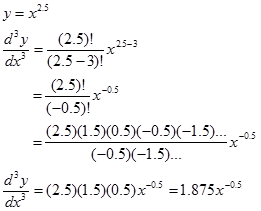
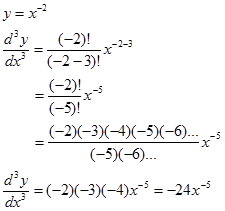
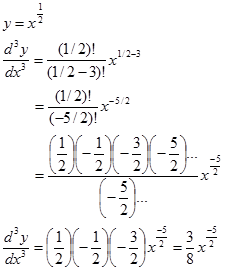









Tidak ada komentar:
Posting Komentar