Suatu persamaan $f(x,y)=0$ pada jangkauan terbatas dari variabel-variabel tertentu dikatakan mendefinisikan $y$ sebagai fungsi $x$ secara implisit.
Contoh 1:
a) Persamaan $xy+x-y-2=0$, dengan $x≠1$ mendefinisikan fungsi $y=\frac{(2-x)}{(x-1)}$.
b) Persamaan $x^{2}+y^{2}-16=0$, mendefinisikan fungsi $y=\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≥0$, dan fungsi $y=-\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≤0$. Perhatikan, lingkarannya harus dianggap terdiri dari dua busur yang bertemu di $(-4,0)$ dan $(4,0)$.
Untuk mendapatkan turunan fungsi implisit caranya turunkan kedua ruas terhadap $x$.
Contoh 2. Cari $y’$ dan $y’’$ pada contoh 1.a. Berapa $y’$ di $x=2$ dan $y’’$ di $x=3$?
Solusi:
Mencari $y’$
Mencari $y’’$
Contoh 3. Cari $y’$ dan $y’’$ pada contoh 1.b. Berapa $y’$ di $x=3$ dan $y’’$ di $x=3$?
Iklan. semoga Anda tertarik
Solusi:
Mencari $y’$
Mencari $y’’$
Contoh 1:
a) Persamaan $xy+x-y-2=0$, dengan $x≠1$ mendefinisikan fungsi $y=\frac{(2-x)}{(x-1)}$.
b) Persamaan $x^{2}+y^{2}-16=0$, mendefinisikan fungsi $y=\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≥0$, dan fungsi $y=-\sqrt{16-x^{2}}$ jika $|x|≤4$ dan $y≤0$. Perhatikan, lingkarannya harus dianggap terdiri dari dua busur yang bertemu di $(-4,0)$ dan $(4,0)$.
Untuk mendapatkan turunan fungsi implisit caranya turunkan kedua ruas terhadap $x$.
Contoh 2. Cari $y’$ dan $y’’$ pada contoh 1.a. Berapa $y’$ di $x=2$ dan $y’’$ di $x=3$?
Solusi:
Mencari $y’$
Mencari $y’’$
Contoh 3. Cari $y’$ dan $y’’$ pada contoh 1.b. Berapa $y’$ di $x=3$ dan $y’’$ di $x=3$?
Iklan. semoga Anda tertarik
Mencari $y’$
Mencari $y’’$

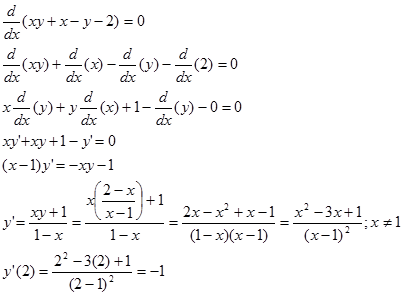
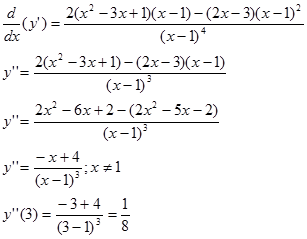
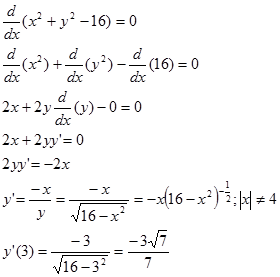










Tidak ada komentar:
Posting Komentar