A. Perkalian suatu bilangan dengan bentuk aljabar
Coba kita ingat kembali sifat distributif pada bilangan bulat.
Jika a, b, dan c bilangan bulat maka berlaku
a(b + c) = ab + ac.
Sifat distributif ini dapat dimanfaatkan untuk menyelesaikan operasi
perkalian pada bentuk aljabar.
Perkalian suku dua (ax + b) dengan skalar k dinyatakan sebagai berikut.
k(ax + b) = kax + kb
Contoh 1. Jabarkan bentuk
perkalian berikut.
a. 2(3x – y)
b. 8(–x²+3x)
Penyelesaian:
Contoh 2. Selesaikan bentuk
perkalian berikut.
a. 2(–6x)
b.
12a(-1/3)
c.
c. (–4x)(–2y)
d.
d. (3a)(–3a)
Penyelesaian:
B. Perkalian antara bentuk aljabar dan bentuk aljabar
Hasil perkalian antara bilangan skalar k dengan suku dua
(ax + b) adalah k (ax + b) = kax + kb.
Dengan memanfaatkan sifat distributif pula, perkalian antara
bentuk aljabar suku dua (ax + b) dengan suku dua (ax + d)
diperoleh sebagai berikut.
Sifat distributif dapat pula digunakan pada perkalian suku dua
dan suku tiga.
Selanjutnya, kita akan membahas mengenai hasil perkalian (ax
+ b) (ax + b), (ax + b)(ax – b), dan (ax – b)(ax
– b). Pelajari uraian berikut ini.
Contoh 3. Tentukan hasil
perkalian bentuk aljabar berikut.
1. (x + 2) (x + 3)
2. (2x + 3) (x²+2x – 5)
Penyelesaian:
1. Cara (i) dengan sifat distributif
Cara (ii) dengan skema
Cara (iii) dengan peragaan mencari luas persegi panjang dengan p
= x + 3 dan l = x + 2 seperti ditunjukkan pada Gambar
di bawah
Maka
2. Cara (i) dengan sifat distributif
Cara (ii) dengan skema







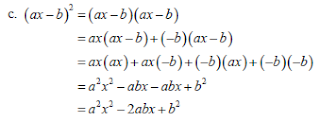

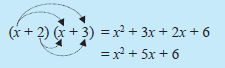













Tidak ada komentar:
Posting Komentar