Misalkan ada dua kejadian A dan B. kalau muncul atau tidak munculnya kejadian A tidak terpengaruh oleh kejadian B, atau sebaliknya. Maka kejadian A dan B semacam itu disebut kejadian saling bebas.
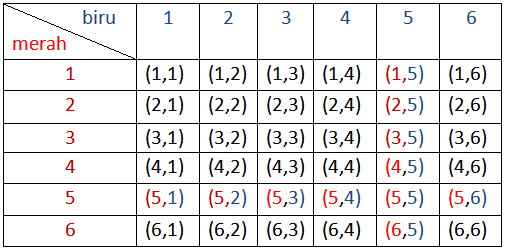
Sebagai contoh, pada percobaan melempar dadu merah dan biru sebanyak satu kali. Kejadian A adalah munculnya bilangan 5 pada dadu merah dan kejadian B adalah munculnya bilangan 5 pada dadu biru, lihat gambar di bawah. Perhatikan bahwa muncul atau tidak munculnya kejadian A tidak terpengaruh oleh kejadian B, begitu juga sebaliknya. Untuk contoh dua kejadian yang saling mempengaruhi, dapat Anda lihat di Menghitung peluang gabungan dua kejadian
Ruang contoh S = {(1,1),(1,2), … ,(6,5),(6,6)}⟹n(S)=36
Kejadian A = {(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)}⟹n(A)=6 ⟹P(A)=P(5 merah)=6/36=1/6
Kejadian B = {(1,5),(2,5),(3,5),(4,5),(5,5),(6,5)}⟹n(B)=6 ⟹ P(B)=P(5 biru)=6/36=1/6
Kejadian A∩B={(5,5)} ⟹n(A∩B) = 1 ⟹ P(A∩B) = P(5 merah dan 5 biru)=1/36
Dari hubungan di atas tampak bahwa
P(5 merah dan 5 biru)= P(5 merah) x P(5 biru)
P(A∩B)= P(A) x P(B)
Meskipun hasil di atas di peroleh dari satu contoh khusus, secara umum hasil itu benar jika dua kejadian itu saling bebas. Dan secara khusus hasil itu tidak benar jika dua kejadian itu tidak saling bebas.
Definisi:
Kejadian A dan kejadian B saling bebas jika dan hanya jika
Jika P(A∩B)≠P(A)×P(B) maka kejadian A dan B tidak saling bebas.
Contoh 1
Dua keping uang logam dilempar sekali. Kejadian A adalah munculnya sisi gambar G pada uang logam pertama dan kejadian B adalah munculnya sisi gambar pada uang logam kedua.
Apakah kejadian A dan B adalah kejadian yang saling bebas ?.
Jawab:
Uang logam mempunyai dua sisi: sisi gambar G dan sisi tulisan T.
Ruang contoh S = {(G,G),(G,T),(T,G),(T,T)} ⟹ n(S)=4.
Kejadian A = {(G,G),(G,T)} ⟹n(A) = 2 ⟹ P(A)=2/4=1/2
Kejadian B = {(G,G),(T,G)} ⟹n(B) = 2 ⟹ P(B)=2/4=1/2
Kejadian A∩B = {(G,G)} ⟹n(A∩B) ⟹ P(A∩B)=1/4=1/2 × 1/2
karena P(A∩B)=P(A)×P(B) maka kejadian A dan B saling bebas.
Contoh 2
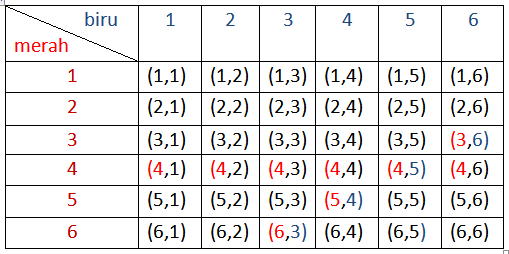
Pada percobaan melempar dadu merah dan biru sebanyak satu kali. Kejadian A adalah munculnya bilangan 4 pada dadu merah dan kejadian B adalah munculnya jumlah bilangan dadu merah dan biru sama dengan 9, lihat gambar
Apakah kejadian A dan B saling bebas ?
Jawab:
Ruang contoh S = {(1,1),(1,2), … ,(6,5),(6,6} ⟹ n(S)=36
Kejadian A = {(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)} ⟹n(A)=6 ⟹P(A)=6/36=1/6
Kejadian B = {(6,3),(5,4),(4,5),(3,6)} ⟹n(B)=4 ⟹P(B)=4/36=1/9
Kejadian A∩B ={(4,5)} ⟹n(A∩B) = 1 ⟹ P(A∩B) = 1/36
Periksa P(A)×P(B)=1/6×1/9=1/54
Tampak bahwa P(A∩B)≠P(A)×P(B)
Jadi, kejadian A dan B tidak saling bebas.
Contoh 3
Kejadian A dan B adalah dua kejadian yang saling bebas, tetapi tidak lepas.
Kalau P(A) = ½ dan P(A⋃B ) = 3/5 , carilah P(B) .
Jawab:
Karena kejadian A dan B saling bebas, maka berlaku
P(A∩B)=P(A)×P(B)
⟹P(A∩B)=1/2 P(B)
Karena kejadian A dan B tidak lepas, maka berlaku
Jadi, peluang kejadian B adalah 1/5.

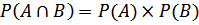
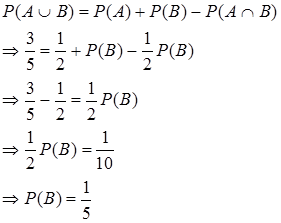









Tidak ada komentar:
Posting Komentar