Peluang kejadian A dengan syarat telah muncul kejadian B adalah
Sedangkan peluang kejadian B dengan syarat telah muncul kejadian A adalah
Contoh 1
Sebuah dadu bersisi enam dilempar sekali. Berapa peluang munculnya bilangan genap kalau sudah diketahui muncul bilangan prima?
Jawab:
Ruang contoh S ={1,2,3,4,5,6} ⇒ n(S) = 6
Kejadian A adalah munculnya bilangan genap, maka A = {2, 4, 6} ⇒ n(A) = 3 ⇒ P(A)=3/6=1/2
Kejadian B adalah munculnya bilangan prima, maka B = {2, 3, 5} ⇒ n(B) = 3 ⇒ P(B)=3/6=1/2
Kejadian A∩B= {2} ⇒ n(A∩B) = 1 ⇒ P(A∩B)=1/6
peluang munculnya bilangan genap kalau sudah diketahui muncul bilangan prima adalah
Jadi, peluangnya P(A|B)=1/3.
Contoh 2
Dadu merah dan biru dilempar sebanyak satu kali. Berapa peluang munculnya bilangan 2 untuk dadu merah kalau telah muncul jumlah mata dadu merah dan biru kurang dari 6 ?
Jawab:
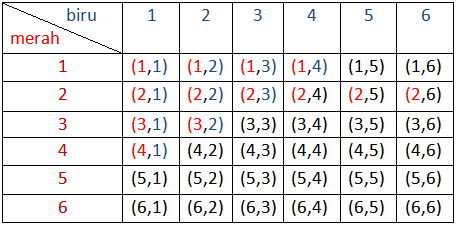
perhatikan gambar
Ruang contoh S = {(1,1),(1,2), … ,(6,5),(6,6} ⇒ n(S)=36
Kejadian A munculnya bilangan 2 untuk dadu merah, maka
A = {(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)} ⇒n(A)=6 ⇒P(A)=6/36=1/6
Kejadian B munculnya jumlah dadu merah dan biru < 6, maka
B = {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)}⇒ n(B)=10 ⇒P(B)=10/36
Kejadian A∩B= {(2,1),(2,2),(2,3)} ⇒n(A∩B) = 3 ⇒ P(A∩B) = 3/36
Peluang munculnya bilangan 2 untuk dadu merah kalau telah muncul jumlah mata dadu merah dan biru kurang dari 6 adalah
Jadi, peluangnya P(A|B)=3/10
Sedangkan peluang kejadian B dengan syarat telah muncul kejadian A adalah
Contoh 1
Sebuah dadu bersisi enam dilempar sekali. Berapa peluang munculnya bilangan genap kalau sudah diketahui muncul bilangan prima?
Jawab:
Ruang contoh S ={1,2,3,4,5,6} ⇒ n(S) = 6
Kejadian A adalah munculnya bilangan genap, maka A = {2, 4, 6} ⇒ n(A) = 3 ⇒ P(A)=3/6=1/2
Kejadian B adalah munculnya bilangan prima, maka B = {2, 3, 5} ⇒ n(B) = 3 ⇒ P(B)=3/6=1/2
Kejadian A∩B= {2} ⇒ n(A∩B) = 1 ⇒ P(A∩B)=1/6
peluang munculnya bilangan genap kalau sudah diketahui muncul bilangan prima adalah
Jadi, peluangnya P(A|B)=1/3.
Contoh 2
Dadu merah dan biru dilempar sebanyak satu kali. Berapa peluang munculnya bilangan 2 untuk dadu merah kalau telah muncul jumlah mata dadu merah dan biru kurang dari 6 ?
Jawab:
perhatikan gambar
Ruang contoh S = {(1,1),(1,2), … ,(6,5),(6,6} ⇒ n(S)=36
Kejadian A munculnya bilangan 2 untuk dadu merah, maka
A = {(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)} ⇒n(A)=6 ⇒P(A)=6/36=1/6
Kejadian B munculnya jumlah dadu merah dan biru < 6, maka
B = {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)}⇒ n(B)=10 ⇒P(B)=10/36
Kejadian A∩B= {(2,1),(2,2),(2,3)} ⇒n(A∩B) = 3 ⇒ P(A∩B) = 3/36
Peluang munculnya bilangan 2 untuk dadu merah kalau telah muncul jumlah mata dadu merah dan biru kurang dari 6 adalah
Jadi, peluangnya P(A|B)=3/10

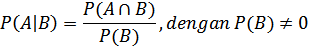
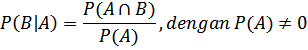
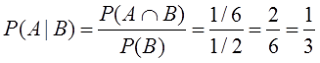
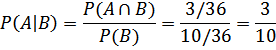










Tidak ada komentar:
Posting Komentar