Untuk menyelesaikan SPLDV dengan metode determinan Crammer, pertama harus dipahami dulu tiga determinan 2x2 yang diambil dari SPLDV
yaitu
1. Determinan utama.
2. Determinan x.
3. Determinan y.
Jika digambarkan pada diagram kartesius, spldv unik adalah dua garis lurus yang berpotongan.
Contoh1. Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1= -1,c1= 9, a2 = 1, b2 = 3 dan c2 = 22
Langkah 2. Hitung nilai D, Dx dan Dy
Langkah 3. Tentukan nilai x dan y
Langkah 4. Himpunan penyelesaian
Jadi, hp={(7,5)}
Himpunan penyelesaian(hp) spldv ini dapat dituliskan sebagai
Jika digambarkan pada diagram kartesius, spldv non unik adalah dua garis lurus yang berimpit.
Contoh2. Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1=3, c1=10, a2 = 8, b2 = 12 dan c2 = 40
Langkah 2. Hitung nilai D, Dx dan Dy
Perhitungan untuk Dx dan Dy tidak perlu dilanjutkan.
Langkah3. Periksa syarat SPLDV non unik
Syarat spldv non unik terpenuhi.
Langka 4. Himpunan penyelesaian.
Dari 2x+3y=10 ambil y=(10-2x)/3.
Jadi, himpunan pemyelesaiannya adalah
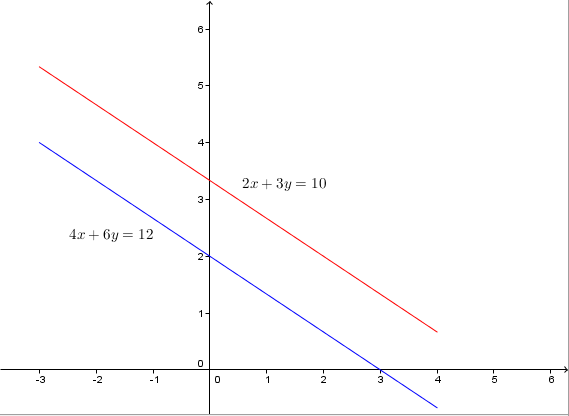
Jika digambarkan pada diagram kartesius, spldv yang tidak mempunyai penyelesaian adalah dua garis lurus yang sejajar.
Contoh3 . Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1=3,c1=10, a2=4, b2=6 dan c2=12
Langkah 2. Hitung nilai D, Dx dan Dy
Perhitungan untuk Dx dan Dy tidak perlu dilanjutkan
Langkah 3. Periksa syarat SPLDV non unik
Salah satu tanda kesamaan tidak terpenuhi. Jadi, spldv tidak mempunyai penyelesaian.
yaitu
1. Determinan utama.
2. Determinan x.
3. Determinan y.
SPLDV Unik
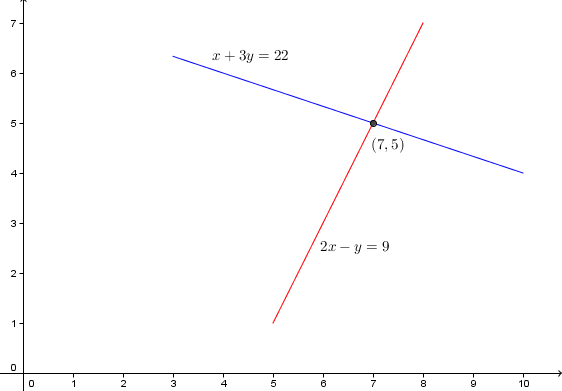
Suatu SPLDV dikatakan unik jika mempunyai solusi tunggal yaitu mempunyai satu pasangan nilai x dan y sebagai penyelesaian. Jika SPLDV mempunyai solusi tunggal maka nilai determinan utamanya tidak nol dan nilai x dan y dapat ditentukan dengan rumusJika digambarkan pada diagram kartesius, spldv unik adalah dua garis lurus yang berpotongan.
Contoh1. Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1= -1,c1= 9, a2 = 1, b2 = 3 dan c2 = 22
Langkah 2. Hitung nilai D, Dx dan Dy
Langkah 3. Tentukan nilai x dan y
Langkah 4. Himpunan penyelesaian
Jadi, hp={(7,5)}
SPLDV Non Unik
Suatu SPLDV dikatakan non unik jika mempunyai solusi banyak yaitu mempunyai tak terhingga pasangan nilai x dan y sebagai penyelesaian. Jika SPLDV mempunyai solusi banyak maka determinan utamanya sama dengan nol dan memenuhi syarat berikut:Himpunan penyelesaian(hp) spldv ini dapat dituliskan sebagai
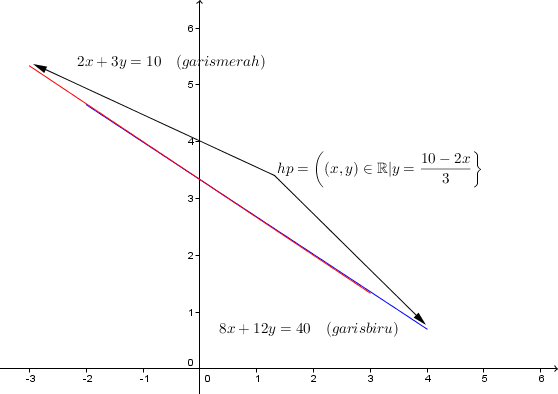
Jika digambarkan pada diagram kartesius, spldv non unik adalah dua garis lurus yang berimpit.
Contoh2. Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1=3, c1=10, a2 = 8, b2 = 12 dan c2 = 40
Langkah 2. Hitung nilai D, Dx dan Dy
Perhitungan untuk Dx dan Dy tidak perlu dilanjutkan.
Langkah3. Periksa syarat SPLDV non unik
Syarat spldv non unik terpenuhi.
Langka 4. Himpunan penyelesaian.
Dari 2x+3y=10 ambil y=(10-2x)/3.
Jadi, himpunan pemyelesaiannya adalah
SPLDV yang tidak mempunyai penyelesaian
Suatu SPLDV dikatakan tidak mempunyai penyelesaian jika tidak mempunyai solusi tunggal atau banyak. Jika SPLDV tidak mempunyai penyelesaian maka determinan utamanya sama dengan nol dan tidak memenuhi syarat SPLDV non unik atau solusi banyak.Jika digambarkan pada diagram kartesius, spldv yang tidak mempunyai penyelesaian adalah dua garis lurus yang sejajar.
Contoh3 . Tentukanlah himpunan penyelesaian system persamaan
Jawab:
Langkah1. Tentukan semua nilai koefisien dan konstanta.
a1=2, b1=3,c1=10, a2=4, b2=6 dan c2=12
Langkah 2. Hitung nilai D, Dx dan Dy
Perhitungan untuk Dx dan Dy tidak perlu dilanjutkan
Langkah 3. Periksa syarat SPLDV non unik
Salah satu tanda kesamaan tidak terpenuhi. Jadi, spldv tidak mempunyai penyelesaian.

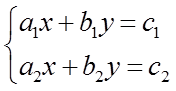
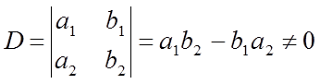
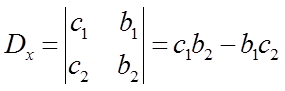
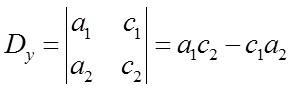
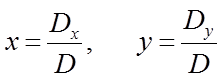
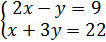
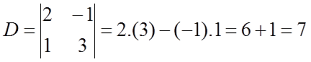
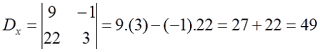
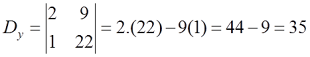
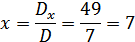
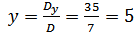
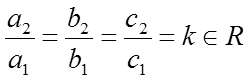
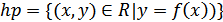
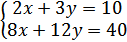
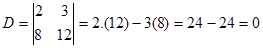


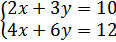
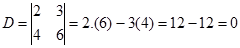
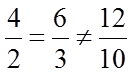









Tidak ada komentar:
Posting Komentar