Pada percobaan melempar dadu berwarna merah yang berisi enam mata sebanyak satu kali dengan ruang contoh S = {1,2,3,4,5,6}. Kejadian A adalah munculnya mata dadu 1 atau 2, A = {1,2}. Dan kejadian B adalah munculnya mata dadu 5 atau 6, B = {5, 6}. Seperti terlihat pada gambar di bawah
Dalam gambar tampak bahwa A dan B adalah dua himpunan yang saling lepas atau himpunan yang saling asing ( disjoint set).
Dalam hal demikian dikatakan bahwa kejadian A dan kejadian B adalah dua kejadian yang saling lepas atau dua kejadian yang saling asing (mutually exlusive) yaitu kejadian A dan kejadian B tidak dapat terjadi secara bersamaan.
Oleh karena A dan B dua kejadian yang saling lepas maka A⋂B = ∅ atau n(A⋂B) = 0 , sehingga P(A⋂B) = 0 .
Dengan memasukkan P(A⋂B) = 0 ke persamaan peluang gabungan, diperoleh
Definisi :
Misalkan A dan B adalah dua kejadian sembarang yang terdapat dalam ruang contoh S yang saling lepas atau terjadi tidak bersamaan, maka peluang gabungan kejadian P(A∪B) adalah
Contoh 1
Sebuah dadu merah bersisi enam, dilemparkan satu kali.
Berapa peluang kejadian munculnya mata dadu ≤ 2 atau munculnya mata dadu ≥ 5 ?
Jawab:
Ruang contoh S pada percobaan tersebut diperlihatkan di bawah
Kejadian A adalah munculnya mata dadu ≤ 2, A = {1,2}⟹ n(A) = 2.
Jadi, P(A)=2/6=1/3
kejadian B adalah munculnya mata dadu ≥ 5, B = {5,6}⟹n(B)=2
Jadi, P(B)=2/6=1/3
Karena A dan B saling lepas, maka
Jadi peluang kejadian munculnya mata dadu ≤ 2 atau munculnya mata dadu ≥ 5 adalah P(A∪B)=2/3.
Contoh 2
Sebuah kartu diambil dari satu set kartu bridge. Berapa peluang yang terambil itu kartu skop atau kartu berwarna merah ?
Jawab:
Satu set kartu bridge terdiri dari 13 kartu cengkih berwarna hitam, 13 kartu hati berwarna merah, 13 kartu berlian berwarna merah, dan 13 kartu skop berwarna hitam.
A adalah kejadian yang terambil itu kartu skop, maka P(A)=13/52.
B adalah kejadian yang terambil itu kartu berwarna merah, maka P(B)=26/52.
Karena A dan B saling lepas, maka
Jadi, peluang yang terambil itu kartu skop atau kartu berwarna merah adalah 3/4.


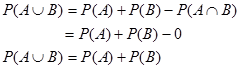


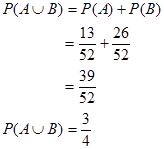










Tidak ada komentar:
Posting Komentar