Tip: Jika rumus tidak jelas pada tampilan mobile/hape, mintalah situs desktop/web pada browser Anda
Definisi:
Untuk tiap $n$ bilangan asli, didefinisikan
Didefinisikan pula $1!=1$ dan $0!=1$.
Tulisan $n!$ dibaca : $n$ factorial.
Contoh 1.
$2!=1×2=2$
$3!=1×2×3=6$
$4!=1×2×3×4=24$
$5!=1×2×3×4×5=120$
$6!=1×2×3×4×5×6=720$
$7!=1×2×3×4×5×6×7=5040$
$8!=1×2×3×4×5×6×7×8=40320$
$9!=1×2×3×4×5×6×7×8×9=362880$
$10!=1×2×3×4×5×6×7×8×9×10=3628800$
Contoh 2.
$7!+6!=5040+720=5760$
$7!-6!=5040-720=4320$
$7!:6!=5040:720=7$
$7!×6!=5040×720=3.628.800$
Jika nilai $n$ makin besar maka nilai $n!$ makin bertambah besar dengan cepat. Untuk $n$ yang besar, nilai faktorial bisa didekati menggunakan rumus Stirling
dimana
$e=2,71828…$ (konstanta alam)
$\pi = 3,14159…$ (konstanta lingkaran)
Contoh 3
Topik Terkait:
Definisi:
Untuk tiap $n$ bilangan asli, didefinisikan
Didefinisikan pula $1!=1$ dan $0!=1$.
Tulisan $n!$ dibaca : $n$ factorial.
Contoh 1.
$2!=1×2=2$
$3!=1×2×3=6$
$4!=1×2×3×4=24$
$5!=1×2×3×4×5=120$
$6!=1×2×3×4×5×6=720$
$7!=1×2×3×4×5×6×7=5040$
$8!=1×2×3×4×5×6×7×8=40320$
$9!=1×2×3×4×5×6×7×8×9=362880$
$10!=1×2×3×4×5×6×7×8×9×10=3628800$
Contoh 2.
$7!+6!=5040+720=5760$
$7!-6!=5040-720=4320$
$7!:6!=5040:720=7$
$7!×6!=5040×720=3.628.800$
Jika nilai $n$ makin besar maka nilai $n!$ makin bertambah besar dengan cepat. Untuk $n$ yang besar, nilai faktorial bisa didekati menggunakan rumus Stirling
dimana
$e=2,71828…$ (konstanta alam)
$\pi = 3,14159…$ (konstanta lingkaran)
Contoh 3
Topik Terkait:

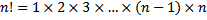
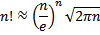










ليست هناك تعليقات:
إرسال تعليق