3. UKURAN PENYEBARAN DATA
A. Rentang
Rentang adalah data terbesar dikurangi data terkecil. Untuk data yang sudah disajikan dalam table frekuensi, rentang dapat dihitung dengan rumus
dimana:
R : rentang
xn : nilai tengah kelas tertinggi
x1 : nilai tengah kelas terendah
Contoh 1. Perhatikan table di bawah !.
Rentangnya adalah
B. Rentang Antar Kuartil
Rentang Antar Kuartil adalah selisih kuartil terbesar dikurangi kiartil terkecil.
dimana:
RAK : rentang antar kuartil
K3 : kuartil ketiga
K1 : kuartil pertama
Contoh 2. Perhatikan table 1!. Jika dihitung , nilai K1 = 69,5 dan K3 = 85,0 (lihat contoh 1 pada pos tentang kuartil, desil dan persentil). Maka
C. Simpangan Kuartil
Simpangan kuartil adalah setengah dari rentang antar kuartil.
Contoh 3. Simpangan kuartil pada table 1 dengan melihat contoh 2 adalah
D. Simpangan Rata-rata
Misalkan kita mempunyai data x1, x2, ..., Xn dengan rataannya . Dengan konsep rentang data kita dapat menentukan rentang tiap data terhadap rataan. Mengingat rentang atau jarak selalu bernilai positif, maka konsep nilai mutlak harus digunakan agar tidak ada jarak yang bernilai negative. Selanjutnya rentang tiap data terhadap rataannya akan berbentuk
Dengan menjumlahkan semua rentang dan membaginya dengan banyak data maka didapat simpangan rata-rata
Untuk data berdistribusi yang memiliki frekuensi dalam tiap interval atau kelompok maka
dimana
SR : simpangan rata-rata
xi : nilai data ke-i (data tunggal) atau nilai tengah kelas ke-i (data berdistribusi)
X : rata-rata
n : banyak data (data tunggal)
fi : frekuensi kelas ke-i (data berdistribusi)
Contoh 4. Diketahui data berikut 75,78,77,80,86. Tentukan simpangan rata-ratanya !
Jawab:
Hitung dulu rata-ratanya
Maka diperoleh simpangan rata-ratanya
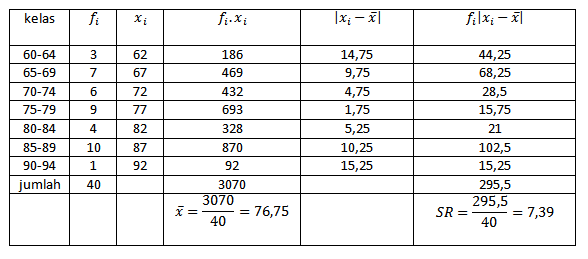
Contoh 5. Tentukan simpangan rata-rata pada table.1
jawab:
Kita ubah tabel 1 dengan memasukan suku-suku yang diperlukan pada simpangan rata-rata
Jadi, simpangan rata-rata SR=7,39.
E. Simpangan Baku dan Ragam (varian)
Menurut ahli statistika, simpangan rata-rata memiliki kelemahan karena menggunakan harga mutlak yang berakibat tidak bisa membedakan antara rentang yang lebih besar dan rentang yang lebih kecil. Untuk mengatasi kelemahan tersebut, ahli statistika memperkenalkan simpangan baku atau standar deviasi (populasi) yang dirumuskan sbb:
dimana
SB : simpangan baku
xi : nilai data ke-i (data tunggal) atau nilai tengah kelas ke-i (data berdistribusi)
fi : frekuensi kelas ke-i (data berdistribusi)
X : rata-rata
n : banyak data
Sedangkan rumus ragam atau varian (populasi) adalah sbb:
dimana Var: ragam atau varian
Simpangan baku dan varian dapat dihubungkan dengan hubungan singkat
Contoh 6. Tentukan a) ragam , dan b) simpangan baku pada table 1!.
Jawab:
Kita ubah tabel 1 dengan memasukan suku-suku yang diperlukan pada simpangan baku dan varian
maka
a) Var = 71,86
b) SB=√71,86 = 8,48
A. Rentang
Rentang adalah data terbesar dikurangi data terkecil. Untuk data yang sudah disajikan dalam table frekuensi, rentang dapat dihitung dengan rumus
dimana:
R : rentang
xn : nilai tengah kelas tertinggi
x1 : nilai tengah kelas terendah
Contoh 1. Perhatikan table di bawah !.
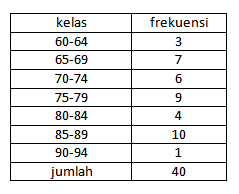 |
| Tabel 1 |
Rentangnya adalah
B. Rentang Antar Kuartil
Rentang Antar Kuartil adalah selisih kuartil terbesar dikurangi kiartil terkecil.
dimana:
RAK : rentang antar kuartil
K3 : kuartil ketiga
K1 : kuartil pertama
Contoh 2. Perhatikan table 1!. Jika dihitung , nilai K1 = 69,5 dan K3 = 85,0 (lihat contoh 1 pada pos tentang kuartil, desil dan persentil). Maka
RAK=85,0-69,5=15,5
C. Simpangan Kuartil
Simpangan kuartil adalah setengah dari rentang antar kuartil.
Contoh 3. Simpangan kuartil pada table 1 dengan melihat contoh 2 adalah
D. Simpangan Rata-rata
Misalkan kita mempunyai data x1, x2, ..., Xn dengan rataannya . Dengan konsep rentang data kita dapat menentukan rentang tiap data terhadap rataan. Mengingat rentang atau jarak selalu bernilai positif, maka konsep nilai mutlak harus digunakan agar tidak ada jarak yang bernilai negative. Selanjutnya rentang tiap data terhadap rataannya akan berbentuk
Dengan menjumlahkan semua rentang dan membaginya dengan banyak data maka didapat simpangan rata-rata
Untuk data berdistribusi yang memiliki frekuensi dalam tiap interval atau kelompok maka
dimana
SR : simpangan rata-rata
xi : nilai data ke-i (data tunggal) atau nilai tengah kelas ke-i (data berdistribusi)
X : rata-rata
n : banyak data (data tunggal)
fi : frekuensi kelas ke-i (data berdistribusi)
Contoh 4. Diketahui data berikut 75,78,77,80,86. Tentukan simpangan rata-ratanya !
Jawab:
Hitung dulu rata-ratanya
Maka diperoleh simpangan rata-ratanya
Contoh 5. Tentukan simpangan rata-rata pada table.1
jawab:
Kita ubah tabel 1 dengan memasukan suku-suku yang diperlukan pada simpangan rata-rata
Jadi, simpangan rata-rata SR=7,39.
E. Simpangan Baku dan Ragam (varian)
Menurut ahli statistika, simpangan rata-rata memiliki kelemahan karena menggunakan harga mutlak yang berakibat tidak bisa membedakan antara rentang yang lebih besar dan rentang yang lebih kecil. Untuk mengatasi kelemahan tersebut, ahli statistika memperkenalkan simpangan baku atau standar deviasi (populasi) yang dirumuskan sbb:
dimana
SB : simpangan baku
xi : nilai data ke-i (data tunggal) atau nilai tengah kelas ke-i (data berdistribusi)
fi : frekuensi kelas ke-i (data berdistribusi)
X : rata-rata
n : banyak data
Sedangkan rumus ragam atau varian (populasi) adalah sbb:
dimana Var: ragam atau varian
Simpangan baku dan varian dapat dihubungkan dengan hubungan singkat
Contoh 6. Tentukan a) ragam , dan b) simpangan baku pada table 1!.
Jawab:
Kita ubah tabel 1 dengan memasukan suku-suku yang diperlukan pada simpangan baku dan varian
maka
a) Var = 71,86
b) SB=√71,86 = 8,48

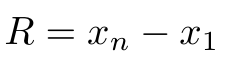



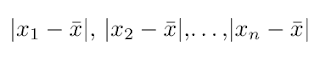
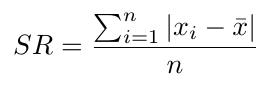
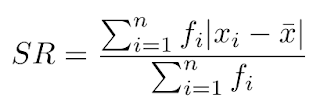

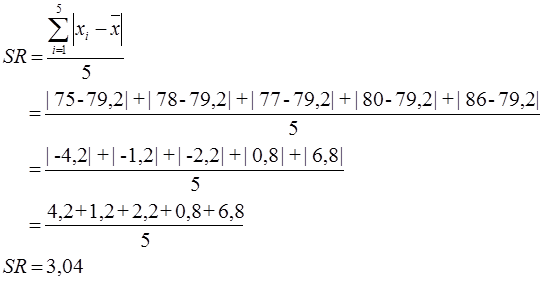

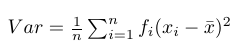
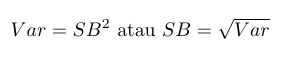










Tidak ada komentar:
Posting Komentar