1. MEMBUAT TABEL FREKUENSI
Langkah-langkah membuat tabel frekwensi adalah sbb:• Cari data terbesar , terkecil dan banyak data. Jika perlu, urutkan data dari yang terkecil sampai yang terbesar.
• Tentukan rentang atau jangkauan data yaitu data terbesar dikurangi data terkecil.
• Tentukan banyak kelas interval dengan rumus Sturgess $k=1+(3,3)\log n$, dimana k banyak kelas dan n banyak data.
• Tentukan panjang kelas dengan rumus $P=\frac{jangkauan}{banyak kelas}$.
Contoh 1. Diketahui data nilai fisika siswa-siswi sebagai berikut
60,60,64,65,66,67,68,69,69,72,74,73,71,70,75,86,77,79,78,90, 87,87,85,87,89,67,77,88,77,78,79,84,82,81,87,80,70,78,86,67.
Buatlah table frekwensinya !
Jawab:
Diketahui data terbesar = 90, data terkecil =60 dan n=40.
jangkauan = 90 - 60 =30.
Banyak kelas k=1+(3,3)log 40 = 6,3 dibulatkan ke 6 atau 7. Disini diambil 7 kelas karena jika diambil 6 kelas maka nilai 90 tidak akan masuk ke kelas manapun.
Panjang kelas P=30/6=5
Selanjutnya atur banyak kelas, panjang kelas sesuai dengan aturan dan banyak data pada tiap interval.
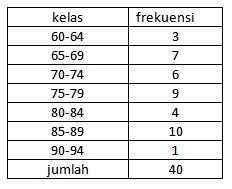
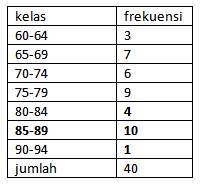
kelas 1 : 60-64, 3 data
kelas 2 : 65-69, 7 data
kelas 3 : 70-74, 6 data
kelas 4 : 75-79, 9 data
kelas 5 : 80-84, 4 data
kelas 6 : 85-89, 10 data
kelas 7 : 90-94, 1 data
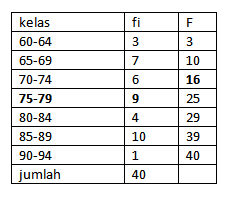
Dari hasil pengolahan data di atas dapat dibentuk ke dalam bentuk table frekuensi
2. UKURAN PEMUSATAN DATA
A. Menentukan Nilai Rataan
Titik tengah interval
Rataan
dimana
𝒙i = data ke-i
𝒇i: frekwensi ke-i
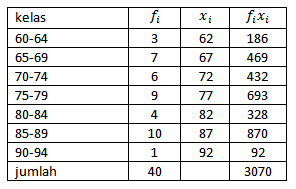
Contoh 2. Hitunglah rataan pada contoh 1
jawab:
Rataan
b. Menentukan Nilai Modus
Rumus
dimana:
Mo: Modus
tb: tepi bawah kelas modus (batas bawah – 0,5)
p: panjang kelas
d1: selisih frekwensi kelas modus dengan kelas sebelumnya
d2: selisih frekwensi kelas modus dengan kelas sesudahnya
Contoh 3. Carilah modus matematika pada contoh 1
Jawab:
Diketahui frekwensi terbanyak adalah 10, maka kelas modus matematika ada di kelas 85-89.
tb=85-0,5=84,5
p=5
d1 = 10-4=6
d2 = 10-1=9
maka
c. Median
Median adalah nilai yang terletak di tengah data yang membagi data menjadi dua bagian yang sama banyaknya.
rumus :
dimana:
Me : median
tb : tepi bawah kelas median (batas bawah – 0,5)
p : panjang kelas
n: banyak data
F : frekwensi kumulatif sebelum kelas median
fm : frekwensi kelas median
Contoh 4. Tentukan median pada contoh 1.
Jawab:
Diketahui data ada 40 maka setengahnya 20, maka letak fm ada dikelas 75-79 (karena di kelas tersebut data sudah melewati 20) maka fm=9.
Sedangkan frekuensi kumulatif F = 3+7+6=16.
tb = 75-0,5=74,5
n=40
p=5
maka

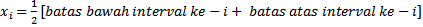
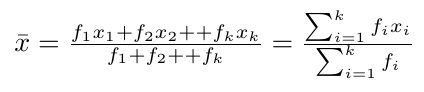
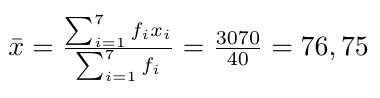
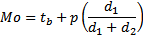
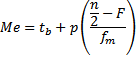









Tidak ada komentar:
Posting Komentar