To find the roots of a quadratic equation by completing the perfect square, the first condition is the coefficient of $x^2$, that is $a$ must be equal to 1 to make it easy to factor. If $a$ is not 1, divide the equation by the coefficient $x^2$ so that $a$ equals 1.
If the term on the left side of the equation appears $x^2+2(\frac{b}{2})x+(\frac{b}{2})^2$, then factor it becomes $(x+\frac{b}{2})^2$.
Which this factoring is valid because $x^2+2(\frac{b}{2})x+(\frac{b}{2})^2=(x+\frac{b}{2})^2$.
Furthermore, the steps to complete a perfect square are as follows:
-On quadratic equations (with $a=1$) $x^2+bx+c=0$, subtract left and right sides by $c$ (if $c <0$, this will be increments)
$x^2+bx+c-c=0-c$
$x^2+bx=-c$
-Modify the term of $bx$ to $2(\frac{b}{2})x$
$x^2+2(\frac{b}{2})x = –c$
-Add the term of $(\frac{b}{2})^2$ on the left and right side
$x^2+2(\frac{b}{2})x+(\frac{b}{2})^2 =(\frac{b}{2})^2–c$
- Change the left side of the equation to $(x+\frac{b}{2})^2$.
$(x+\frac{b}{2})^2=(\frac{b}{2})^2–c$
- Take the roots of the left and right segments
$x+\frac{b}{2}=±√((\frac{b}{2})^2–c)$
- Subtract left and right sides by $\frac{b}{2}$ (if $b <0$, this will be increments)
The ± sign means that the formula handles two operations, namely addition, and subtraction.
The root $𝑥₁$ is obtained by taking the plus sign (+):
-Root $𝑥₂$ is obtained by taking the minus sign (-) :
Example 1. Find the roots of the equations
$x^2-5x+4=0$
$x^2+7x+12=0$
Answer:
Example 2. Find the roots of the equations
$2x^2-7x+3=0$
$6x^2-5x-6=0$
Answer:

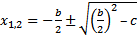
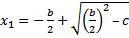
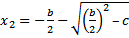
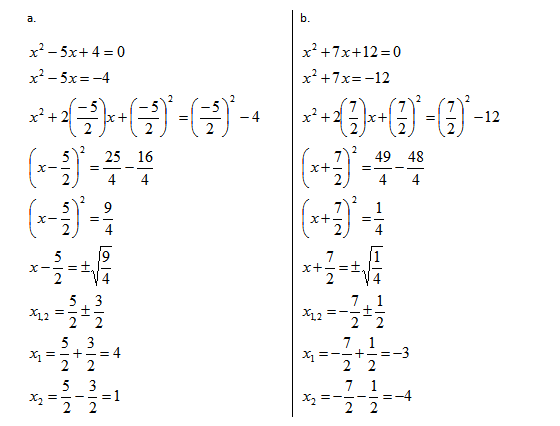











ليست هناك تعليقات:
إرسال تعليق