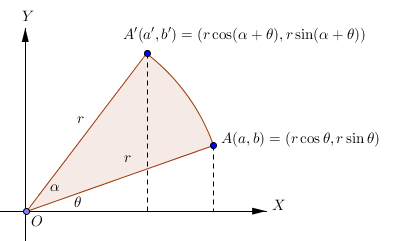
Rotasi geometri adalah perpindahan suatu benda dengan cara berputar terhadap titik tertentu (bukan dirinya) yang disebut pusat rotasi.
Pada rotasi geometri, jarak titik awal terhadap titik pusat rotasi sama dengan jarak titik akhir terhadap titik pusat rotasi.
Secara umum rotasi geometri terdiri dari dua macam yaitu rotasi terhadap titik awal O(0,0) dan rotasi terhadap titik P(m, n) dimana m dan n bukan nol.
Titik A(a,b) berotasi sebesar sudut alfa dan kedudukannya sekarang adalah A’(a’,b’). yang jadi pertanyaan adalah bagaimana hubungan a’dan b’ terhadap a dan b?. untuk itu kita akan menggunakan bantuan definisi dasar trigonometri yaitu sbb:
Dengan menggunakan rumus jumlah sudut cosinus dan mengganti suku $r\cos\theta$ oleh a dan $r\sin\theta $ oleh b maka hubunganga a’ dengan a dan b adalah
Dengan menggunakan rumus jumlah sudut sinus dan mengganti suku $r\cos\theta $ oleh a dan $r\sin\theta $ oleh b maka hubunganga b’ dengan a dan b adalah
Jika kedua hubungan terakhir dituliskan dalam bentuk matriks maka
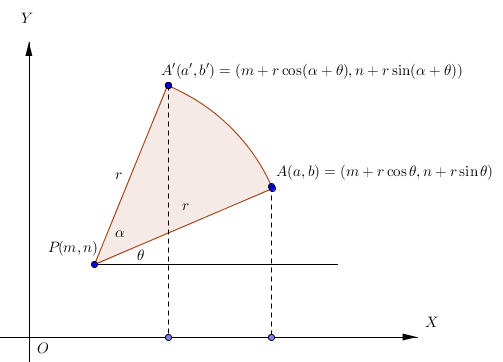
Titik A(a,b) berotasi sebesar sudut alfa terhadap P(m,n) dan kedudukannya sekarang adalah A’(a’,b’). yang jadi pertanyaan adalah bagaimana hubungan a’, b’ dengan a, b?. untuk itu kita akan menggunakan bantuan definisi dasar trigonometri yaitu sbb:
Dengan menggunakan rumus jumlah sudut cosinus dan mengganti suku $r\cos\theta$ oleh $a-m$ dan $r\sin\theta$ oleh $b-n$ maka hubunganga a’ dengan a dan b adalah
Dengan menggunakan rumus jumlah sudut sinus dan mengganti suku $r\cos\theta$ oleh $a-m$ dan $r\sin\theta$ oleh $b-n$ maka hubunganga b’ dengan a dan b adalah
Jika kedua hubungan terakhir dituliskan dalam bentuk matriks maka
Contoh 1. Tentukan bayangan titik $A(4,7)$ oleh rotasi $30^o$ terhadap titik pusat
Jawab:
Jadi bayangannya adalah $A’(\frac{4\sqrt{3}-7}{2}, \frac{4+7\sqrt{3}}{2})$.
Contoh 2. Tentukan bayangan titik $A(4,7)$ oleh rotasi $30^o$ terhadap titik $P(1,2)$
Jawab:
Jadi bayangannya adalah $A’(\sqrt{3}, 5+2\sqrt{2})$.
1. Rotasi terhadap titik asal O(0,0)
Perhatikan gambar berikutTitik A(a,b) berotasi sebesar sudut alfa dan kedudukannya sekarang adalah A’(a’,b’). yang jadi pertanyaan adalah bagaimana hubungan a’dan b’ terhadap a dan b?. untuk itu kita akan menggunakan bantuan definisi dasar trigonometri yaitu sbb:
Dengan menggunakan rumus jumlah sudut cosinus dan mengganti suku $r\cos\theta$ oleh a dan $r\sin\theta $ oleh b maka hubunganga a’ dengan a dan b adalah
Dengan menggunakan rumus jumlah sudut sinus dan mengganti suku $r\cos\theta $ oleh a dan $r\sin\theta $ oleh b maka hubunganga b’ dengan a dan b adalah
Jika kedua hubungan terakhir dituliskan dalam bentuk matriks maka
2. Rotasi terhadap titik P(m, n)
Perhatikan gambar berikutTitik A(a,b) berotasi sebesar sudut alfa terhadap P(m,n) dan kedudukannya sekarang adalah A’(a’,b’). yang jadi pertanyaan adalah bagaimana hubungan a’, b’ dengan a, b?. untuk itu kita akan menggunakan bantuan definisi dasar trigonometri yaitu sbb:
Dengan menggunakan rumus jumlah sudut cosinus dan mengganti suku $r\cos\theta$ oleh $a-m$ dan $r\sin\theta$ oleh $b-n$ maka hubunganga a’ dengan a dan b adalah
Dengan menggunakan rumus jumlah sudut sinus dan mengganti suku $r\cos\theta$ oleh $a-m$ dan $r\sin\theta$ oleh $b-n$ maka hubunganga b’ dengan a dan b adalah
Jika kedua hubungan terakhir dituliskan dalam bentuk matriks maka
Contoh 1. Tentukan bayangan titik $A(4,7)$ oleh rotasi $30^o$ terhadap titik pusat
Jawab:
Jadi bayangannya adalah $A’(\frac{4\sqrt{3}-7}{2}, \frac{4+7\sqrt{3}}{2})$.
Contoh 2. Tentukan bayangan titik $A(4,7)$ oleh rotasi $30^o$ terhadap titik $P(1,2)$
Jawab:
Jadi bayangannya adalah $A’(\sqrt{3}, 5+2\sqrt{2})$.

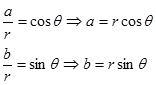
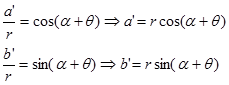
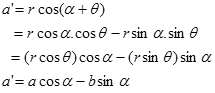
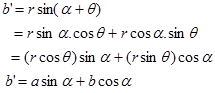
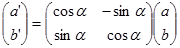
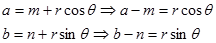
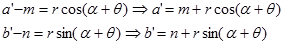
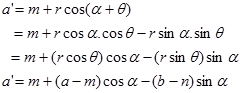
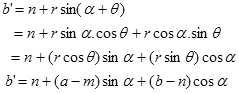
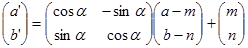
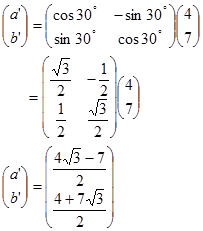
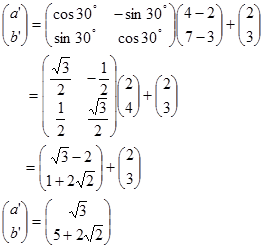









Tidak ada komentar:
Posting Komentar