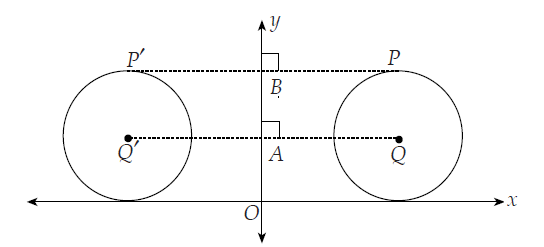
Perhatikan lingkaran Q yang dicerminkan terhadap sumbu-y berikut ini.
Dari gambar tersebut, dapat disimpulkan bahwa:
• Lingkaran Q kongruen dengan bayangannya, yaitu lingkaran Q’.
• Jarak setiap titik pada lingkaran Q ke cermin sama dengan jarak setiap titik bayangannya ke cermin, yaitu QA = Q’A dan PB = P’B.
• Sudut yang dibentuk oleh cermin dengan garis yang menghubungkan setiap titik ke bayangannya adalah sudut siku-siku.
Sifat-sifat tersebut merupakan sifat-sifat refleksi. Dengan menggunakan sifat-sifat ini, kita dapat menentukan bayangan sebuah titik yang dicerminkan terhadap suatu garis atau terhadap suatu titik lain.
1. Pencerminan terhadap titik asal
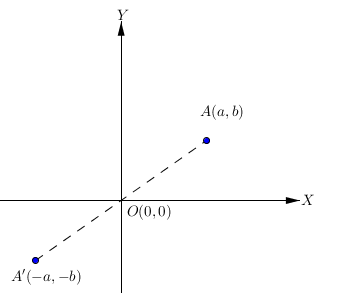
Pencerminan titik A(a, b) terhadap titik asal O(0,0) menghasilkan bayangan titik A’(-a, -b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah ,
sehingga persamaan (1) dapat dirumuskan sebagai
2. Pencerminan terhadap sumbu-x
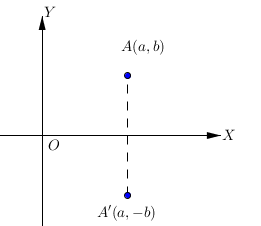
Pencerminan titik A(a, b) terhadap sumbu-x menghasilkan bayangan titik A’(a, -b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (2) dapat dirumuskan sebagai
3. Pencerminan terhadap sumbu-y
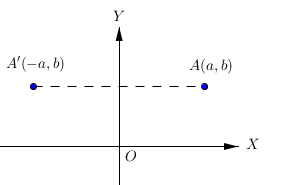
Pencerminan titik A(a, b) terhadap sumbu-y menghasilkan bayangan titik A’(-a, b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (3) dapat dirumuskan sebagai
4. Pencerminan terhadap garis y = x
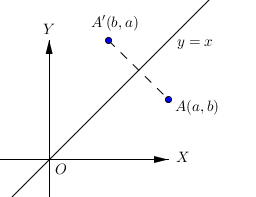
Pencerminan titik A(a, b) terhadap garis y = x menghasilkan bayangan titik A’(b, a).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (4) dapat dirumuskan sebagai
5. Pencerminan terhadap garis y = -x
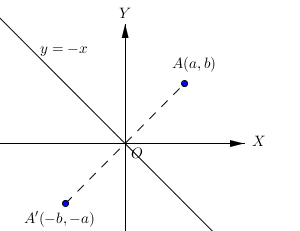
Pencerminan titik A(a, b) terhadap garis y = -x menghasilkan bayangan titik A’(-b, -a).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (5) dapat dirumuskan sebagai
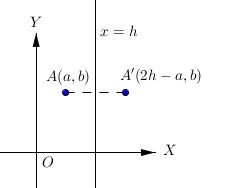
6. Pencerminan terhadap garis x = h
Pencerminan titik A(a, b) terhadap garis x h menghasilkan bayangan titik A’(2h-a, b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
namun ini tidak cukup untuk menyatakannya dalam bentuk matriks karena hanya menghasilkan titik (-a, b) sehingga harus ditambah matriks kolom
Persamaan (6) menjadi
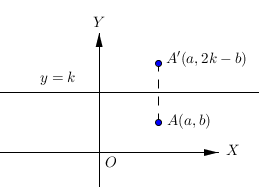
7. Pencerminan terhadap garis y
Pencerminan titik A(a, b) terhadap garis y k menghasilkan bayangan titik A’(a, 2k-b).
Secara matematis dirumuskan dengan
Jika ditulis dalam matriks transformasi persamaan (7) dapat dirumuskan sebagai
Contoh. 1. Tentukan bayangan segitiga ABC dengan titik sudut A(-2, 4), B(0, 5), dan C(3, 2) jika a. dicerminkan terhadap titik asal
b. dicerminkan terhadap sumbu-x
c. dicerminkan terhadap sumbu-y
d. dicerminkan terhadap garis y=x
e. dicerminkan terhadap garis y=-x
f. dicerminkan terhadap garis x=2.
g. dicerminkan terhadap garis y=1.
Jawab:
a. Pencerminan terhadap titik asal O(0,0)
Jadi, bayangan segitiga ABC oleh pencerminan terhadap titik asal adalah segitiga A’B’C’dengan titik sudut A’(2,-4), B’(0,5), dan C’(-3,-2).
b. Pencerminan terhadap sumbu-x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap sumbu-x adalah segitiga A’B’C’dengan titik sudut A’(-2,-4), B’(0,5), dan C’(3,-2).
c. Pencerminan terhadap sumbu-y
Jadi, bayangan segitiga ABC oleh pencerminan terhadap sumbu-y adalah segitiga A’B’C’dengan titik sudut A’(2,4), B’(0,-5), dan C’(-3,2).
d. Pencerminan terhadap garis y=x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=x adalah segitiga A’B’C’dengan titik sudut A’(4,-2), B’(-5,0), dan C’(2,3).
e. dicerminkan terhadap garis y=-x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=-x adalah segitiga A’B’C’dengan titik sudut A’(-4,2), B’(5,0), dan C’(-2,-3).
f. dicerminkan terhadap garis x=2.
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis x=2 adalah segitiga A’B’C’dengan titik sudut A’(6, 4), B’(4, -5), dan C’(1, 2).
g. dicerminkan terhadap garis y=1.
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=1 adalah segitiga A’B’C’dengan titik sudut A’(-2,-2), B’(0,7), dan C’(3,0).
Dari gambar tersebut, dapat disimpulkan bahwa:
• Lingkaran Q kongruen dengan bayangannya, yaitu lingkaran Q’.
• Jarak setiap titik pada lingkaran Q ke cermin sama dengan jarak setiap titik bayangannya ke cermin, yaitu QA = Q’A dan PB = P’B.
• Sudut yang dibentuk oleh cermin dengan garis yang menghubungkan setiap titik ke bayangannya adalah sudut siku-siku.
Sifat-sifat tersebut merupakan sifat-sifat refleksi. Dengan menggunakan sifat-sifat ini, kita dapat menentukan bayangan sebuah titik yang dicerminkan terhadap suatu garis atau terhadap suatu titik lain.
1. Pencerminan terhadap titik asal
Pencerminan titik A(a, b) terhadap titik asal O(0,0) menghasilkan bayangan titik A’(-a, -b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah ,
sehingga persamaan (1) dapat dirumuskan sebagai
2. Pencerminan terhadap sumbu-x
Pencerminan titik A(a, b) terhadap sumbu-x menghasilkan bayangan titik A’(a, -b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (2) dapat dirumuskan sebagai
3. Pencerminan terhadap sumbu-y
Pencerminan titik A(a, b) terhadap sumbu-y menghasilkan bayangan titik A’(-a, b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (3) dapat dirumuskan sebagai
4. Pencerminan terhadap garis y = x
Pencerminan titik A(a, b) terhadap garis y = x menghasilkan bayangan titik A’(b, a).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (4) dapat dirumuskan sebagai
5. Pencerminan terhadap garis y = -x
Pencerminan titik A(a, b) terhadap garis y = -x menghasilkan bayangan titik A’(-b, -a).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
sehingga persamaan (5) dapat dirumuskan sebagai
6. Pencerminan terhadap garis x = h
Pencerminan titik A(a, b) terhadap garis x h menghasilkan bayangan titik A’(2h-a, b).
Secara matematis dirumuskan dengan
Matriks transformasi untuk pencerminan ini adalah
namun ini tidak cukup untuk menyatakannya dalam bentuk matriks karena hanya menghasilkan titik (-a, b) sehingga harus ditambah matriks kolom
Persamaan (6) menjadi
7. Pencerminan terhadap garis y
Pencerminan titik A(a, b) terhadap garis y k menghasilkan bayangan titik A’(a, 2k-b).
Secara matematis dirumuskan dengan
Jika ditulis dalam matriks transformasi persamaan (7) dapat dirumuskan sebagai
Contoh. 1. Tentukan bayangan segitiga ABC dengan titik sudut A(-2, 4), B(0, 5), dan C(3, 2) jika a. dicerminkan terhadap titik asal
b. dicerminkan terhadap sumbu-x
c. dicerminkan terhadap sumbu-y
d. dicerminkan terhadap garis y=x
e. dicerminkan terhadap garis y=-x
f. dicerminkan terhadap garis x=2.
g. dicerminkan terhadap garis y=1.
Jawab:
a. Pencerminan terhadap titik asal O(0,0)
Jadi, bayangan segitiga ABC oleh pencerminan terhadap titik asal adalah segitiga A’B’C’dengan titik sudut A’(2,-4), B’(0,5), dan C’(-3,-2).
b. Pencerminan terhadap sumbu-x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap sumbu-x adalah segitiga A’B’C’dengan titik sudut A’(-2,-4), B’(0,5), dan C’(3,-2).
c. Pencerminan terhadap sumbu-y
Jadi, bayangan segitiga ABC oleh pencerminan terhadap sumbu-y adalah segitiga A’B’C’dengan titik sudut A’(2,4), B’(0,-5), dan C’(-3,2).
d. Pencerminan terhadap garis y=x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=x adalah segitiga A’B’C’dengan titik sudut A’(4,-2), B’(-5,0), dan C’(2,3).
e. dicerminkan terhadap garis y=-x
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=-x adalah segitiga A’B’C’dengan titik sudut A’(-4,2), B’(5,0), dan C’(-2,-3).
f. dicerminkan terhadap garis x=2.
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis x=2 adalah segitiga A’B’C’dengan titik sudut A’(6, 4), B’(4, -5), dan C’(1, 2).
g. dicerminkan terhadap garis y=1.
Jadi, bayangan segitiga ABC oleh pencerminan terhadap garis y=1 adalah segitiga A’B’C’dengan titik sudut A’(-2,-2), B’(0,7), dan C’(3,0).

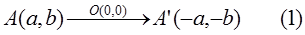
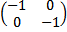

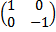
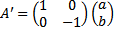
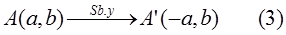
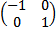
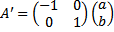
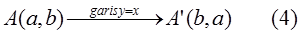
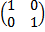
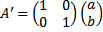








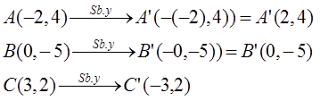














Tidak ada komentar:
Posting Komentar