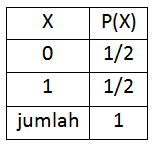
Ketika melakukan eksperimen acak melambungkan sebuah mata uang yang homogen kita mendapatkan peluang muncul angka P(A) dan peluang muncul gambar P(G) adalah P(A)=P(G)=1/2. Kalau dihitung banyak gambar yang tampak maka A=0⨉G dan G=1⨉G. kalau banyak muka G diberi simbol X maka untuk muka A berlaku X=0 dan muka G berlaku X=1. Kita dapatkan notasi baru untuk peluang yaitu P(X = 0)=1/2 dan P(X=1)=1/2.
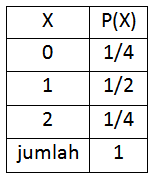
Kalau eksperimen acak dilakukan pada dua buah mata uang, maka peristiwa yang mungkin terjadi adalah: AA, AG, GA, GG. Jika X menyatakan banyak muka G, maka X=0,1,2. Sehingga deretan peluangnya adalah P(X=0)=1/4, P(X=1)=1/2 dan P(X=2)=1/4.
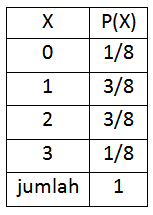
Kalau eksperimen acak dilakukan pada dua buah mata uang, maka peristiwa yang mungkin terjadi adalah: AAA, AAG, AGA, AGG, GAA, GAG, GGA, GGG. . Jika X menyatakan banyak muka G, maka X=0,1,2,3. Sehingga deretan peluangnya adalah P(X=0)=1/8, P(X=1)=3/8 , P(X=2)=3/8 dan P(X=3)=1/8.
Eksperimen ini dapat diteruskan dengan menggunakan lebih banyak uang logam
Dalam keadaan demikian, jumlah semua peluang selalu sama dengan satu. Apabila hal ini terjadi , maka dikatakan bahwa distribusi peluang untuk variabel acak X telah terbentuk.
Jadi, Variabel acak diskrit $X$ menentukan distribusi peluang apabila untuk nilai-nilai $X=x_{1}, x_{2},…,x_n$ terdapat peluang $p(x_{i})=P(X= x_{i})$ sehingga
$p(x)$ adalah fungsi peluang untuk variabel acak $X$ pada saat harga $X=x$.
Untuk sebuah variabel acak diskrit kita dapat menentukan ekspektasi(harapan)nya, jika ada. Dengan rumus
$\epsilon(X)$ adalah ekspektasi variabel acak $X$ dan penjumlahan dikerjakan untuk semua harga $X$ yang mungkin. $\epsilon(X)$ adalah rata-rata untuk variabel acak $X$.
Contoh 1. Pengamatan di sebuah pos polisi lalu lintas memperlihatkan bahwa banyak kendaraan yang melewati sebuah tikungan setiap menit mengikuti distribusi peluang sbb:
Tentukan
a) Paling sedikit ada 4 kendaraan per menit
b) Paling banyak ada 4 kendaraan per menit
c) Rata-rata kendaraan per menit
Solusi
a)Paling sedikit ada 4 kendaraan per menit maka
b)Paling banyak ada 4 kendaraan per menit maka
c) Rata-rata kendaraan per menit maka
Atau 331 kendaraan tiap 100 menit.
jika $X$ adalah variabel acak kontinyu, maka kita mempunyai fungsi densitas(kepadatan) peluang $f(x)$ yang dapat menghasilkan peluang untuk harga-harga x. Dalam hal ini berlaku
Untuk menentukan peluang harga $X=x$ misalnya antara a dan b dgunakan rumus
Ekspektasi variabel acak kontinyu $X$ ditentukan dengan rumus
Atau dengan batas-batas lainnya.
Contoh 2. Masa pakai sebuah lampu $X$ dinyatakan dengan fungsi densitas eksponensial sebagai
Dimana $e=2,7183$ dan $x$ dalam bulan.
Tentukan
a)peluang lampu $X$ dapat dipakai 3 sampai 4 bulan
b)peluang lampu $X$ dapat dipakai lebih dari 4 bulan
c)rata-rata masa pakai lampu $X$
Solusi
a)peluang lampu $X$ dapat dipakai 3 sampai 4 bulan
Jadi peluangnya 0,3129
b)peluang lampu $X$ dapat dipakai lebih dari 4 bulan
Jadi peluangnya 0,7908
c)rata-rata masa pakai lampu $X$
Jadi, rata-rata masa pakainya adalah 9 bulan.
Kalau eksperimen acak dilakukan pada dua buah mata uang, maka peristiwa yang mungkin terjadi adalah: AA, AG, GA, GG. Jika X menyatakan banyak muka G, maka X=0,1,2. Sehingga deretan peluangnya adalah P(X=0)=1/4, P(X=1)=1/2 dan P(X=2)=1/4.
Kalau eksperimen acak dilakukan pada dua buah mata uang, maka peristiwa yang mungkin terjadi adalah: AAA, AAG, AGA, AGG, GAA, GAG, GGA, GGG. . Jika X menyatakan banyak muka G, maka X=0,1,2,3. Sehingga deretan peluangnya adalah P(X=0)=1/8, P(X=1)=3/8 , P(X=2)=3/8 dan P(X=3)=1/8.
Eksperimen ini dapat diteruskan dengan menggunakan lebih banyak uang logam
1.Variabel acak diskrit
Simbol X pada percobaan- percobaan di atas yang memiliki peluang bersifat variabel dan memiliki harga harga 0, 1, 2, 3, … . variabel seperti itu dimana tiap nilai variabelnya memiliki peluang disebut variabel acak diskrit(random discrete variable).Dalam keadaan demikian, jumlah semua peluang selalu sama dengan satu. Apabila hal ini terjadi , maka dikatakan bahwa distribusi peluang untuk variabel acak X telah terbentuk.
Jadi, Variabel acak diskrit $X$ menentukan distribusi peluang apabila untuk nilai-nilai $X=x_{1}, x_{2},…,x_n$ terdapat peluang $p(x_{i})=P(X= x_{i})$ sehingga
$p(x)$ adalah fungsi peluang untuk variabel acak $X$ pada saat harga $X=x$.
Untuk sebuah variabel acak diskrit kita dapat menentukan ekspektasi(harapan)nya, jika ada. Dengan rumus
$\epsilon(X)$ adalah ekspektasi variabel acak $X$ dan penjumlahan dikerjakan untuk semua harga $X$ yang mungkin. $\epsilon(X)$ adalah rata-rata untuk variabel acak $X$.
Contoh 1. Pengamatan di sebuah pos polisi lalu lintas memperlihatkan bahwa banyak kendaraan yang melewati sebuah tikungan setiap menit mengikuti distribusi peluang sbb:
Tentukan
a) Paling sedikit ada 4 kendaraan per menit
b) Paling banyak ada 4 kendaraan per menit
c) Rata-rata kendaraan per menit
Solusi
a)Paling sedikit ada 4 kendaraan per menit maka
b)Paling banyak ada 4 kendaraan per menit maka
c) Rata-rata kendaraan per menit maka
Atau 331 kendaraan tiap 100 menit.
2. Variabel acak kontinyu
variabel acak yang tidak diskrit disebut Variabel acak kontinyu (random continous variable). Variabel jenis ini digunakan untuk menyatakan besaran seperti waktu dan hasil pengukuran. Jadi, jika $X$ adalah variabel acak kontinyu, maka harga $X=x$ dibatasi oleh $-∞<x<∞$ atau batas-batas lain.jika $X$ adalah variabel acak kontinyu, maka kita mempunyai fungsi densitas(kepadatan) peluang $f(x)$ yang dapat menghasilkan peluang untuk harga-harga x. Dalam hal ini berlaku
Untuk menentukan peluang harga $X=x$ misalnya antara a dan b dgunakan rumus
Ekspektasi variabel acak kontinyu $X$ ditentukan dengan rumus
Atau dengan batas-batas lainnya.
Contoh 2. Masa pakai sebuah lampu $X$ dinyatakan dengan fungsi densitas eksponensial sebagai
Dimana $e=2,7183$ dan $x$ dalam bulan.
Tentukan
a)peluang lampu $X$ dapat dipakai 3 sampai 4 bulan
b)peluang lampu $X$ dapat dipakai lebih dari 4 bulan
c)rata-rata masa pakai lampu $X$
Solusi
a)peluang lampu $X$ dapat dipakai 3 sampai 4 bulan
Jadi peluangnya 0,3129
b)peluang lampu $X$ dapat dipakai lebih dari 4 bulan
Jadi peluangnya 0,7908
c)rata-rata masa pakai lampu $X$
Jadi, rata-rata masa pakainya adalah 9 bulan.


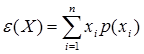

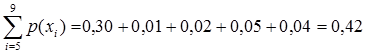
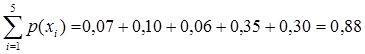

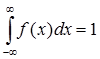
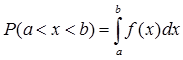



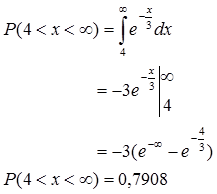











Tidak ada komentar:
Posting Komentar