Contoh Masalah Operasi Aljabar pada Fungsi
Seorang fotografer dapat menghasilkan gambar yang bagus melalui dua tahap, yaitu tahap pemotretan dan tahap editing. Biaya yang diperlukan pada tahap pemotretan (P) adalah adalah Rp.500 per gambar (g), mengikuti fungsi:
$P(g) = 500g + 2.500$,
dan biaya pada tahap editing (E) adalah Rp.1000 per gambar , mengikuti fungsi
$E(g) = 1000g + 500$,
dengan g adalah banyak gambar yang dihasilkan.
a) Berapakah total biaya yang diperlukan untuk menghasilkan 10 gambar dengan kualitas yang bagus?
b) Tentukanlah selisih antara biaya pada tahap pemotretan dengan biaya pada tahap editing untuk 5 gambar.
Penyelesaian
Diketahui
Fungsi biaya pemotretan: $P(g) = 500g + 2.500$.
Fungsi biaya editing $E(g) = 1000g + 3000$.
a) Gambar yang bagus dapat diperoleh melalui dua tahap proses yaitu pemotretan dan editing, sehingga fungsi biaya yang dihasilkan adalah
$P(g)+ E(g) = (500g + 2.500) + (1000g + 3000) = 1500g + 5500$
Total biaya untuk menghasilkan 10 gambar (g = 10) adalah
$P(10)+ E(10) = (1500 × 10) + 5500 = 20500$
Jadi, total biaya yang diperlukan untuk menghasilkan 10 gambar dengan kualitas yang bagus adalah Rp.20500.
b) Selisih biaya tahap editing dengan tahap pemotretan adalah
$E(g)–P(g) = (1000g + 3000) –(500g + 2.500) = 500g +500$
Selisih biaya pemotretan dengan biaya editing untuk 5 gambar (g = 5) adalah
$E(5) – P(5) = (500 × 5) + 500 = 2500$.
Jadi, selisih biaya yang diperlukan untuk menghasilkan 5 gambar dengan kualitas yang bagus adalah Rp.2500.
Definisi Operasi aljabar pada fungsi:
Jika $f$ suatu fungsi dengan daerah asal $D_f$ dan g suatu fungsi dengan daerah asal $D_g$, maka pada operasi aljabar penjumlahan, pengurangan, perkalian, dan pembagian dinyatakan sebagai berikut.1. Jumlah $f$ dan $g$ ditulis $f+g$ didefinisikan sebagai
$(f+g)(x) = f(x)+g(x)$
dengan daerah asal $D_{f+g} = D_{f}∩D_{g}$.
2. Selisih $f$ dan $g$ ditulis $f-g$ didefinisikan sebagai
$(f -g)(x) = f(x)-g(x)$
dengan daerah asal $D_{f-g} = D_{f}∩D_{g}$.
3. Perkalian $f$ dan $g$ ditulis $f×g$ didefinisikan sebagai
$(f×g)(x) = f(x)×g(x)$
dengan daerah asal $D_{f×g} = D_{f}∩D_{g}$.
4. Pembagian $f$ dan $g$ ditulis $\frac{f}{g}$ didefinisikan sebagai
$\frac{f}{g}(x)=\frac{f(x)}{g(x)}$
dengan daerah asal $D_{\frac{f}{g}} = D_{f}∩D_{g}$, $g(x)\neq 0$.
Contoh 1. Diketahui fungsi $f(x) = x + 3$ dan $g(x)= x^{2} – 9$. Tentukanlah fungsi-fungsi berikut dan tentukan pula daerah asalnya.
a) Penjumlahan fungsi b) Pengurangan fungsi c) Perkalian fungsi d) Pembagian fungsi
Penyelesaian
Daerah asal fungsi $f(x) = x + 3$ adalah $D_f $={𝒙 | 𝒙∈R} dan daerah asal fungsi $g(x)= x^{2} – 9$ adalah $D_g$ = {𝒙 | 𝒙∈R}.
a) Penjumlahan
$(f+g)(x)=(x + 3)+(x^{2} – 9)=x^{2}+x– 6$.
Daerah asal fungsi $(f+g)(x)$ adalah
$D_{f +g}=D_{f }⋂D_{g}$ = {𝒙 | 𝒙∈R}⋂{𝒙 | 𝒙∈R}={𝒙 | 𝒙∈R}
b) Pengurangan
$(f-g)(x)=(x + 3)-(x^{2} – 9)=-x^{2}+x+12$.
Daerah asal fungsi $(f + g)(x)$ adalah
$D_{f-g}=D_{f }⋂D_{g}$ = {𝒙 | 𝒙∈R}⋂{𝒙 | 𝒙∈R}={𝒙 | 𝒙∈R}
c) Perkalian
$(f×g)(x)=(x + 3)×(x^{2} – 9)=x^{3}+3x^{2}-9x-27$.
Daerah asal fungsi $(f×g)(x)$ adalah
$D_{f×g}=D_{f }⋂D_{g}$ = {𝒙 | 𝒙∈R}⋂{𝒙 | 𝒙∈R}={𝒙 | 𝒙∈R}
d) Pembagian
$(\frac{f}{g})(x)=\frac{(x + 3)}{(x^{2} – 9)}=\frac{1}{x-3}$.
Daerah asal fungsi $(f×g)(x)$ adalah
$D_{\frac{f}{g}}=D_{f }⋂D_{g}$ dan $x^{2} – 9\neq0$
= {𝒙 | 𝒙∈R}⋂{𝒙 | 𝒙∈R}dan $x^{2} – 9\neq0$
={𝒙≠3 atau 𝒙≠ -3| 𝒙∈R}
Contoh 2. Diketahui fungsi $f(x)=\sqrt{x^{2}-4}$ dan $f(x)=\sqrt{x+2}. Tentukanlah fungsi-fungsi berikut dan tentukan pula daerah asalnya.
a) Penjumlahan fungsi b) Pengurangan fungsi c) Perkalian fungsi d) Pembagian fungsi
Penyelesaian:
Daerah asal fungsi adalah dan daerah asal fungsi adalah
Penyelesaian:
Daerah asal fungsi adalah dan daerah asal fungsi adalah
dan

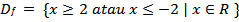
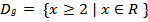
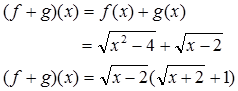
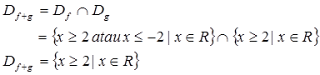
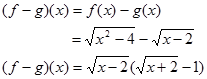
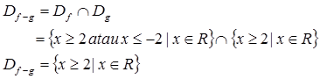
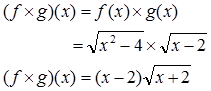
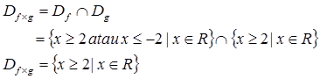
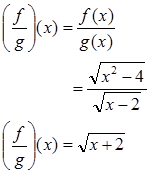










Tidak ada komentar:
Posting Komentar