Logaritma adalah suatu operasi matematika khusus yang bertujuan mencari nilai pangkat yang digunakan pada bilangan basis dan hasil yang diketahui. Jadi, logaritma adalah invers dari eksponen. Logaritma dituliskan dengan “log” dan didefinisikan sebagai berikut.
Definisi:
Misalkan $a,b,c$ adalah bilangan real, $a>0, a≠1$ dan $b > 0$, maka
$^{a}\log{b}=c$ Jika dan hanya jika $a^{b} = c$.
Dimana $a$ disebut basis
$b$ disebut numerus $(b>0)$
$c$ disebut hasil logaritma
Catatan:
1. Ada dua versi penempatan basis logaritma yaitu versi Indonesia, basis ditulis di sisi kiri atas kata “log” yaitu $^{a}\log{b}$ . Dan versi internasional, basis ditulis di sisi kanan bawah kata “log” yaitu $\log_{a}b$. Untuk selanjutnya akan dipakai versi Indonesia saja.
2. Untuk logaritma basis 10, sudah menjadi kesepakatan umum basisnya tidak dituliskan. Jadi, $^{10}\log{b}$ cukup ditulis $\log{b}$ saja.
3. Untuk logaritma basis bilangan alam atau natural $e$ ($e≈2,718…, e$ disebut juga bilangan Euler), sudah menjadi kesepakatan umum $^{e}\log{b}$ diganti dengan $\ln{b}$. Jadi, kalau bertemu $\ln{b}$ itu berarti $\ln{b}=^{e}\log b$ , $\ln{x}=^{e}\log x$ , dan sebagainya.
Contoh 1
Tanda “⇔” dibaca “jika dan hanya jika” adalah operator logika biimplikasi. Untuk menanamkan pemahaman awal konsep logaritma, kata “jika dan hanya jika” untuk sementara bisa diganti dengan kata “karena”. Meskipun secara ilmu logika mungkin kurang tepat, namun dalam bahasa sehari-hari bisa lebih familiar. Misalnya pada contoh 1.b, $^{2}\log{8}=3$ karena $2^{3} = 8$.
Contoh 2. Dengan menggunakan definisi logaritma, tentukan nilai-nilai logaritma berikut
Jawab:
a) Misal $^{2}\log{64}=x$. Maka
$^{2}\log{64}=x$⇔$2^{x}=64$
Dengan menggunakan persamaan pangkat sederhana
$2^{x}=64$
$2^{x}=2^6$
⇔$x=6$
Jadi, $^{2}\log{64}=6$.
b) Misal $^{\frac{1}{2}}\log{64}=x$. Maka
$^{\frac{1}{2}}\log{64}=x$⇔ $(\frac{1}{2})^{x}=64$
Dengan menggunakan persamaan pangkat sederhana
$(\frac{1}{2})^{x}=64$
$(2^{-1})^{x}=2^6$
$2^{-x}=2^{6}$
⇔$-x=6$
$x=-6$
Jadi, $^{\frac{1}{2}}\log{64}=-6$.
c) Misal $^{3}\log{81}=x$. Maka
$^{3}\log{81}=x$⇔ $3^{x}=81$
Dengan menggunakan persamaan pangkat sederhana
$3^{x}=81$
$3^{x}=3^4$
Jadi, $^{3}\log{81}=4$.
d) Misal $\log{0,001}=x$. Maka
$\log{0,001}$ ⇔ $10^{x}=0,001$
Dengan menggunakan persamaan pangkat sederhana
$10^{x}=0,001$
$10^{x}=\frac{1}{1000}$
$10^{x}=\frac{1}{10^{3}}$
$10^{x}=10^{-3}$
$x=-3$
Jadi, $\log{0,001}=-3$

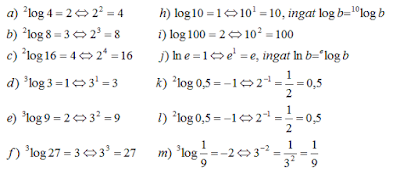
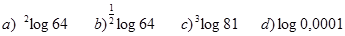









Tidak ada komentar:
Posting Komentar