Tip: Jika rumus tidak jelas pada tampilan mobile/hape, mintalah situs desktop/web pada browser Anda
Barisan Geometri
Suatu arisan $u_1, u_2, …, u_n$ disebut barisan geometri jika mempunyai nilai pembanding atau rasio yang tetap antara satu suku dengan satu suku berikutnya, yaitu
dengan $r$ bilangan tetap yang disebut rasio, yang tidak tergantung pada $n$. Barisan ini mempunyai rumus suku ke-n
dimana $u_n$ : suku ke n
$n = 1,2,3, …$
$a$ : suku awal
$r$ : rasio
Contoh 1 . Carilah suku pertama, rasio dan suku ke-6 pada dua barisan berikut
a) $5, 10, 20,40, …$
b) $4, 2, 1, 1/2, …$
Jawab:
a) Suku pertama $a = 5$, rasio $r=\frac{10}{5}=2$. Suku ke-6 nya $u_6 = 5.2^5=160$
b) Suku pertama $a = 4$, rasio $\frac{2}{4}=\frac{1}{2}$ Suku ke-6 nya $4(\frac{1}{2})^5=\frac{1}{8}$
Contoh 2. Suku kedua barisan Geometri adalah 6, sedangkan suku ke sebelasnya adalah 3072.
a) Carilah suku pertama dan rasionya
b) Tentukanlah rumus suku ke-n nya
Jawab:
a) $u_2=6⇒ar=6$....1
$u_{10}=3072⇒ar^{10}=3072$....2
bagi persamaan (2) oleh persamaan (1), didapat $r=2$.
Tukarkan $r=2$ ke persamaan (1) atau (2), didapat $a=3$.
Jadi, suku pertamanya 9 dan rasionya 3
b) rumus suku ke-n nya $u_n=3.2^{n-1}$
Suku tengah
Perhatikan barisan-barisan Geometri berikut. Banyak suku pada tiap barisan ini ganjil.
a) $u_1, u_2, u_3$; banyak suku 3 dan suku tengahnya $u_2$. Suku tengah $u_2$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_2=ar=\sqrt{a^2r^2} =\sqrt{a.ar^2} =\sqrt{u_1.u_3}$
b) $u_1, u_2, u_3, u_4, u_5$; banyak suku 5 dan suku tengahnya $u_3$.
Suku tengah $u_3$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_3=ar^2=\sqrt{a^2r^4} =\sqrt{a.ar^4} =\sqrt{u_1.u_5}$
Secara umum untuk barisan geometri $u_1, … , u_k, … , u_{2k-1}$; banyak suku $2k-1, k>=2, k$ bilangan asli, suku tengahnya $u_k$ dapat dirumuskan sbb:
$u_k=ar^{k-1} =\sqrt{a^2r^{2(k-1})}=\sqrt{a.ar^{2(k-1})}= \sqrt{u_1.u_{2k-1}}$
Sedangkan untuk barisan geometri dengan banyak sukunya genap, itu tidak mempunyai suku tengah.
Contoh 3. Diketahui barisan $3, 9,…,243,$. Banyak suku barisan itu ganjil.
a) Cari suku tengahnya
b) Suku ke berapakah itu ?
c) Berapa banyak suku barisan itu ?
Jawab:
Diketahui $a = 3, r=3$, suku terakhir $ u_{2k-1}=243$
a) $u_k=\sqrt{u_1.u_{2k-1}}=\sqrt{3.243}=\sqrt{729}=27$
b) $u_k=3.3^{k-1}=27$ ,
⇒$3.3^{k-1}=27\\
\quad 3^{k-1}=9\\
\quad 3^{k-1}=3^2\\
\quad k-1=2\\
\quad k=3$
c) Banyak suku barisan itu $2k-1=2.3-1=6-1=5$ suku
Sisipan
Misalkan di antara dua bilangan ril $a$ dan $c$ ($a\neq c$) disisipkan sebanyak $k$ buah bilangan ($k$ bilangan asli), sehingga bilangan-bilangan campuran membentuk barisan geometri. Pertanyaannya adalah berapakah rasio barisan geometri yang terbentuk itu ?. Untuk menjawab pertanyaan itu, kita misalkan rasionya $r$. Dengan pemisalan itu, barisan geometri yang terbentuk dapat digambarkan sbb:
Untuk menentukan rasionya, bagikan suku terakhir oleh suku sebelummya
$r=\frac{c}{ar^k}$
⇒$ar^{k+1}=c$
⇒$r^{k+1}=\frac{c}{a}$
Untuk $k$ genap, nilai $r$ hanya ada satu kemungkinan yaitu
Untuk $k$ ganjil, nilai $r$ mempunyai dua kemungkinan yaitu
Contoh 4. Carilah rasio barisan geometri yang terbentuk, dan tuliskan deretnya jika
a) antara $\frac{1}{4}$ dan $32$ disispkan $6$ bilangan
b) antara $2$ dan $512$ disispkan $3$ bilangan
Jawab:
a) $a=\frac{1}{4}$ , $c=32$ dan $k=6$. $r=\sqrt[6+1]{\frac{32}{\frac{1}{4}}}=\sqrt[7]{128}=2 $
barisannya $\frac{1}{4},\frac{1}{2},1,2,4,8,16,32$
b) $a=2$, $c = 512$ dan $k =3$. $r= \sqrt[3+1]{\frac{512}{2}}=\sqrt[4]{256}=4 $
barisannya $2, 8, 32, 128,512$
dan
$r= -\sqrt[3+1]{\frac{512}{2}}=-\sqrt[4]{256}=-4$
barisannya $2, -8, 32, -128,512$
Deret Geometri
Jika barisan $u_1, u_2, …, u_n$ adalah barisan geometri maka $u_1 + u_2 +…+ u_n$ adalah deret Geometri. Jumlah n suku pertama deret geometri adalah
Kalikan kedua ruas pada persamaan (1) oleh $r$
Kurangkan persamaan (2) oleh persamaan (1), diperoleh
Contoh 5 . Carilah jumlah tiap deret geometri berikut
a) Jumlah 10 suku pertama deret $1+2+4+…$
b) Jumlah 10 suku pertama deret $8+4+2+…$
c) Jumlah tak terhingga deret $8+4+2+…$
Jawab:
a) $a=1$, $r=2>1$. Maka $S_{10}=\frac{1(2^{10}-1)}{2-1}=\frac{2^{10}-1}{1}=1023$
b) $a=8$, $r=\frac{1}{2}<1$. Maka $S_{10}=\frac{8(1-(\frac{1}{2})^{10})}{1-\frac{1}{2}}=\frac{2^{10}-1}{2^6}=\frac{1023}{64}$
c) $S_∞=\frac{8}{1-\frac{1}{2}}=\frac{8}{\frac{1}{2}}=16$
Barisan Geometri
Suatu arisan $u_1, u_2, …, u_n$ disebut barisan geometri jika mempunyai nilai pembanding atau rasio yang tetap antara satu suku dengan satu suku berikutnya, yaitu
$\frac{u_n}{u_{n-1}}=r$
dengan $r$ bilangan tetap yang disebut rasio, yang tidak tergantung pada $n$. Barisan ini mempunyai rumus suku ke-n
dimana $u_n$ : suku ke n
$n = 1,2,3, …$
$a$ : suku awal
$r$ : rasio
Contoh 1 . Carilah suku pertama, rasio dan suku ke-6 pada dua barisan berikut
a) $5, 10, 20,40, …$
b) $4, 2, 1, 1/2, …$
Jawab:
a) Suku pertama $a = 5$, rasio $r=\frac{10}{5}=2$. Suku ke-6 nya $u_6 = 5.2^5=160$
b) Suku pertama $a = 4$, rasio $\frac{2}{4}=\frac{1}{2}$ Suku ke-6 nya $4(\frac{1}{2})^5=\frac{1}{8}$
Contoh 2. Suku kedua barisan Geometri adalah 6, sedangkan suku ke sebelasnya adalah 3072.
a) Carilah suku pertama dan rasionya
b) Tentukanlah rumus suku ke-n nya
Jawab:
a) $u_2=6⇒ar=6$....1
$u_{10}=3072⇒ar^{10}=3072$....2
bagi persamaan (2) oleh persamaan (1), didapat $r=2$.
Tukarkan $r=2$ ke persamaan (1) atau (2), didapat $a=3$.
Jadi, suku pertamanya 9 dan rasionya 3
b) rumus suku ke-n nya $u_n=3.2^{n-1}$
Suku tengah
Perhatikan barisan-barisan Geometri berikut. Banyak suku pada tiap barisan ini ganjil.
a) $u_1, u_2, u_3$; banyak suku 3 dan suku tengahnya $u_2$. Suku tengah $u_2$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_2=ar=\sqrt{a^2r^2} =\sqrt{a.ar^2} =\sqrt{u_1.u_3}$
b) $u_1, u_2, u_3, u_4, u_5$; banyak suku 5 dan suku tengahnya $u_3$.
Suku tengah $u_3$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_3=ar^2=\sqrt{a^2r^4} =\sqrt{a.ar^4} =\sqrt{u_1.u_5}$
Secara umum untuk barisan geometri $u_1, … , u_k, … , u_{2k-1}$; banyak suku $2k-1, k>=2, k$ bilangan asli, suku tengahnya $u_k$ dapat dirumuskan sbb:
$u_k=ar^{k-1} =\sqrt{a^2r^{2(k-1})}=\sqrt{a.ar^{2(k-1})}= \sqrt{u_1.u_{2k-1}}$
Sedangkan untuk barisan geometri dengan banyak sukunya genap, itu tidak mempunyai suku tengah.
Contoh 3. Diketahui barisan $3, 9,…,243,$. Banyak suku barisan itu ganjil.
a) Cari suku tengahnya
b) Suku ke berapakah itu ?
c) Berapa banyak suku barisan itu ?
Jawab:
Diketahui $a = 3, r=3$, suku terakhir $ u_{2k-1}=243$
a) $u_k=\sqrt{u_1.u_{2k-1}}=\sqrt{3.243}=\sqrt{729}=27$
b) $u_k=3.3^{k-1}=27$ ,
⇒$3.3^{k-1}=27\\
\quad 3^{k-1}=9\\
\quad 3^{k-1}=3^2\\
\quad k-1=2\\
\quad k=3$
c) Banyak suku barisan itu $2k-1=2.3-1=6-1=5$ suku
Sisipan
Misalkan di antara dua bilangan ril $a$ dan $c$ ($a\neq c$) disisipkan sebanyak $k$ buah bilangan ($k$ bilangan asli), sehingga bilangan-bilangan campuran membentuk barisan geometri. Pertanyaannya adalah berapakah rasio barisan geometri yang terbentuk itu ?. Untuk menjawab pertanyaan itu, kita misalkan rasionya $r$. Dengan pemisalan itu, barisan geometri yang terbentuk dapat digambarkan sbb:
Untuk menentukan rasionya, bagikan suku terakhir oleh suku sebelummya
$r=\frac{c}{ar^k}$
⇒$ar^{k+1}=c$
⇒$r^{k+1}=\frac{c}{a}$
⇒$r=(\frac{c}{a})^{\frac{1}{ k+1}}=\sqrt[k+1]{\frac{c}{a}} $
Untuk $k$ genap, nilai $r$ hanya ada satu kemungkinan yaitu
$ r=\sqrt[k+1]{\frac{c}{a} } $
Untuk $k$ ganjil, nilai $r$ mempunyai dua kemungkinan yaitu
$ r=\sqrt[k+1]{\frac{c}{a}} $ dan $ r=-\sqrt[k+1]{\frac{c}{a}} $
Contoh 4. Carilah rasio barisan geometri yang terbentuk, dan tuliskan deretnya jika
a) antara $\frac{1}{4}$ dan $32$ disispkan $6$ bilangan
b) antara $2$ dan $512$ disispkan $3$ bilangan
Jawab:
a) $a=\frac{1}{4}$ , $c=32$ dan $k=6$. $r=\sqrt[6+1]{\frac{32}{\frac{1}{4}}}=\sqrt[7]{128}=2 $
barisannya $\frac{1}{4},\frac{1}{2},1,2,4,8,16,32$
b) $a=2$, $c = 512$ dan $k =3$. $r= \sqrt[3+1]{\frac{512}{2}}=\sqrt[4]{256}=4 $
barisannya $2, 8, 32, 128,512$
dan
$r= -\sqrt[3+1]{\frac{512}{2}}=-\sqrt[4]{256}=-4$
barisannya $2, -8, 32, -128,512$
Deret Geometri
Jika barisan $u_1, u_2, …, u_n$ adalah barisan geometri maka $u_1 + u_2 +…+ u_n$ adalah deret Geometri. Jumlah n suku pertama deret geometri adalah
$S_n = a+ar +ar^2 +…+ar^{n-1}$ ……..(1)
Kalikan kedua ruas pada persamaan (1) oleh $r$
$rS_n = ar+ar^2 +ar^3 +…+ar^n$ ……..(2)
Kurangkan persamaan (2) oleh persamaan (1), diperoleh
$rS_n - S_n = ar^n - a$
$(1- r)S_n = a(r^n -1)$
Jika $r<1$, maka
Khusus untuk $r<1$ jika $n$ menuju tak terhingga, maka jumlahnya
Contoh 5 . Carilah jumlah tiap deret geometri berikut
a) Jumlah 10 suku pertama deret $1+2+4+…$
b) Jumlah 10 suku pertama deret $8+4+2+…$
c) Jumlah tak terhingga deret $8+4+2+…$
Jawab:
a) $a=1$, $r=2>1$. Maka $S_{10}=\frac{1(2^{10}-1)}{2-1}=\frac{2^{10}-1}{1}=1023$
b) $a=8$, $r=\frac{1}{2}<1$. Maka $S_{10}=\frac{8(1-(\frac{1}{2})^{10})}{1-\frac{1}{2}}=\frac{2^{10}-1}{2^6}=\frac{1023}{64}$
c) $S_∞=\frac{8}{1-\frac{1}{2}}=\frac{8}{\frac{1}{2}}=16$



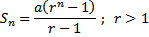
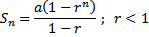











Tidak ada komentar:
Posting Komentar