Metode substitusi adalah suatu metode untuk memecahkan sebuah sistem persamaan dengan cara menukarkan variabel. Secara harfiah, substitusi diserap dari bahasa Inggris “substitution” yang berarti pertukaran. Untuk menguasai metode substitusi, diharuskan menguasai aljabar terlebih dahulu agar tidak mengalami kebingungan dalam prosesnya.
Agar langkah-langkah penyelesaian SPLTV dengan metode substitusi atau pertukaran variabel mudah dipahami, mari perhatikan SPLTV berikut
Untuk menyelesaikan SPLTV dengan metode substitusi ditempuh langkah-langkah sbb:
Langkah 1
Pilih persamaan yang mempunyai varabel dengan nilai mutlak koefisien/pengali terkecil. Jika ada beberapa, pilih yang mana saja.
Pada SPLTV diatas, variabel yang koefisiennya paling kecil adalah y dan z pada persamaan 1 dan z pada persamaan 2. Kita pilih persamaan 1 saja 2x+y+z=26.
Langkah 2
Ubah persamaan terpilih menjadi bentuk persamaan explisit. Variabel dengan koefisien terkecil sebagai variabel terikat, kita pilih $z$
Langkah 3
Masukan persamaan(4) pada persamaan yang bukan asalnya, berarti ke persamaan 2 dan 3.
- pada persamaan 2.
-pada persamaan 3.
Langkah 4
Jadikan persamaan 5 dan 6 sebagai SPLDV
Langkah 5
Cari penyelesaian SPLDV itu dengan metode substitusi, eliminasi atau determinan.
--dengan metode substitusi SPLDV
Dari persamaan 6 ambil $y=25-2x$ …(7)
Masukan persamaan 7 ke persamaan 5
Masukan x=10 ke persamaan 7
--dengan metode determinan SPLDV.
Terlihat hasilnya sama, jadi bisa dipilih metode mana yang menurut kalian mudah.
Langkah 6
Masukan nilai x dan y ke persamaan 4
Langkah 7
Tuliskan himpunan penyelesaian SPLTV dalam bentuk HP={(nilai x, nilai y, nilai z)}, atau jawaban akhir tergantung permintaan soal.
Jadi, himpunan penyelesaian SPLTV-nya adalah HP={(10,5,1)}.
Langkah-langkah penyelesaian SPLTV di atas adalah untuk soal yang tidak berbentuk soal cerita. Untuk soal yang berbentuk soal cerita, langkah pertama adalah membuat model matematika dari permasalahan terlebih dahulu. Seperti dua contoh berikut.
Contoh 1. Unyil, Ucrit dan Usro belanja tiga jenis pakaian yang sama di sebuah toko. Unyil membeli 2 kaos, 2 celana levis, 3 kemeja dan membayar Rp.340rb. Ucrit membeli 3 kaos, 1 celana levis, 2 kemeja dan membayar Rp.230rb. Usro membeli 4 kaos, 3 celana levis, 2 kemeja dan membayar Rp.430rb. Tentukan harga masing-masing kaos, celana levis dan kemeja.
Penyelesaian:
Kita misalkan harga kaos =x, celana levis = y, kemeja = z.
Unyil membeli 2 kaos, 2 celana levis, 3 kemeja dan membayar Rp.340rb.
2x+2y+3z=340rb...(1)
Ucrit membeli 3 kaos, 1 celana levis, 2 kemeja dan membayar Rp.230rb.
3x+y+2z=230rb...(2)
Usro membeli 4 kaos, 3 celana levis, 2 kemeja dan membayar Rp.430rb.
4x+3y+2z=430rb...(3)
Buat model matematikanya sbb:
Langkah 1
Pilih persamaan yang mempunyai nilai mutlak koefisien/pengali terkecil, jika ada. Pada SPLTV diatas, variabel yang koefisiennya paling kecil adalah y pada persamaan 2.
3x+y+2z=230rb.
Langkah 2
Ubah persamaan terpilih menjadi bentuk persamaan explisit dengan y sebagai variabel terikat. Namai persamaan ini sebagai persamaan(4) atau persamaan sementara.
Langkah 3
Masukan persamaan(4) pada persamaan yang bukan asalnya, berarti ke persamaan 1 dan 3.
--pada persamaan 1.
--pada persamaan 3.
Langkah 4
Jadikan persamaan 5 dan 6 sebagai SPLDV
Langkah 5
Cari penyelesaian SPLDV itu dengan metode substitusi, eliminasi atau determinan.
Disini akan digunkan metode determinan SPLDV.
Langkah 6
Masukan nilai x dan z ke persamaan 4
Langkah 7.
Jadi, harga kaos Rp.20rb, celana levis Rp.90rb, dan kemeja Rp.40rb.
Contoh 2. Sebuah fungsi kubik (pangkat tiga) melewati titik-titik A(0,-2), B(1,2), C(2,4), D(3,10). Tentukan fungsi tersebut
Penyelesaian:
Bentuk umum fungsi kubik adalah
Pada x = 0, y = -2
Pada x = 3 , y = 10
Untuk menemukan nilai a,b,c bentuklah persamaan1,2, dan 3 ke dalam SPLTV sbb:
Pilih persamaan yang mempunyai nilai mutlak koefisien/pengali terkecil. Pada SPLTV diatas, kita pilih persamaan 1.
a+b+c=4.
Langkah 2
Ubah persamaan terpilih menjadi bentuk persamaan explisit dengan c sebagai variabel terikat.
Langkah 3
Masukan persamaan(4) pada persamaan 2 dan 3.
--pada persamaan 2.
--pada persamaan 3.
Langkah 4
Jadikan persamaan 5 dan 6 sebagai SPLDV
Langkah 5
Cari penyelesaian SPLDV itu dengan metode substitusi, eliminasi atau determinan.
Disini akan digunkan metode substitusi SPLDV.
Dari persamaan 6 didapat b = -4a, masukan pada persamaan 5
Maka $b= -4$.
Langkah 6
Masukan nilai a dan b ke persamaan 4
Langkah 7
Masukan nilai a,b,c dan d ke bentuk umum fungsi kubik.
Bentuk fungsi kubik dalam kasus ini adalah
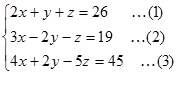
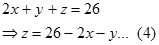
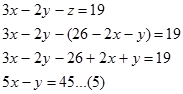
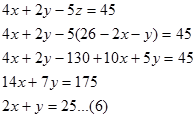
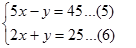
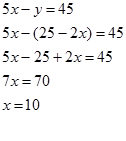
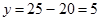
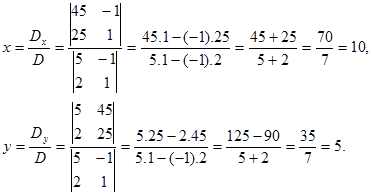
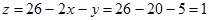
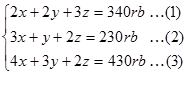
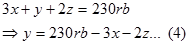
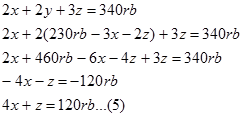
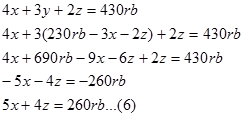
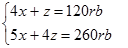
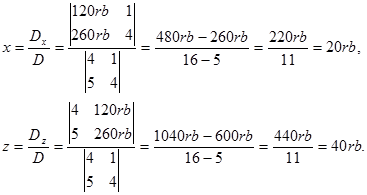
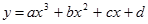
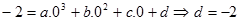
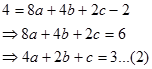
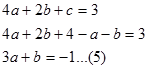
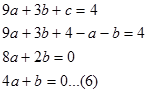
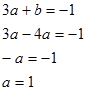
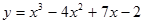
Tidak ada komentar:
Posting Komentar