1. Relativitas Newton
Suatu benda dikatakan bergerak apabila kedudukan benda itu berubah terhadap kedudukan tertentu. Untuk menyatakan benda itu bergerak kita harus menentukan suatu titik acuan atau kerangka acuan yang digunakan sebagai patokan. Sebagai contoh, Asep pergi ke Jakarta dengan naik kereta api, menurut pengamat yang berdiri diam di stasiun mengatakan Asep itu bergerak, sedangkan menurut pengamat yang duduk di sebelah Asep di dalam kereta itu mengatakan Asep itu diam tidak bergerak. Jadi dalam hal ini Asep dapat dikatakan diam atau bergerak tergantung pada titik acuan atau kerangka acuan yang dipakai. Apabila kerangka acuan adalah stasiun dikatakan Asep bergerak, tetapi jika kerangka acuan yang digunakan adalah kereta api maka Asep itu dikatakan diam.
Berdasarkan contoh di atas benda yang bergerak itu bersifat relatif, yaitu tergantung pada kerangka acuan yang digunakan. Dalam peristiwa di atas terdapat dua kerangka acuan, yaitu kerangka acuan yang diam (kerangka acuan yang dipakai oleh pengamat yang ada di stasiun) dan kerangka acuan yang bergerak (kerangka acuan yang dipakai oleh pengamat yang ada di dalam kereta api yang bergerak). Stasiun kereta api yang kita anggap diam ini pun sebenarnya juga bergerak bersama-sama bumi mengelilingi matahari, matahari bersama-sama bintang-bintang yang lainnya bergerak dalam galaksi dan begitu seterusnya. Dengan demikian gerak benda itu tidak mutlak melainkan bersifat relatif.
Dalam keadaan-keadaan demikian, relativitas Newton menyatakan bahwa:
Semua hukum Fisika (Mekanika Newton) berlaku untuk semua kerangka acuan inersial, sedangkan kecepatan benda tergantung pada kerangka acuan tanpa ada pembatasan untuk kecepatan relativistic (mendekati kecepatan cahaya).
2. Transformasi Galileo
Untuk menyatakan kedudukan sebuah titik atau benda kita memerlukan satu sistem koordinat atau kerangka acuan. Misalnya untuk menyatakan sebuah benda yang bergerak, seorang pengamat memerlukan suatu kerangka acuan dengan sistem koordinat misalnya (x, y, z). Jadi kerangka acuan adalah suatu sistem koordinat (x, y, z) di mana seorang pengamat melakukan pengamatan suatu kejadian. Dalam hal ini kita gunakan kerangka acuan inersial di mana hukum Newton berlaku.
Kerangka acuan inersial yaitu suatu kerangka acuan yang berada dalam keadaan diam atau bergerak dengan kecepatan konstan (tetap) terhadap kerangka acuan lain pada garis lurus. Untuk menyatakan hubungan antara pengamatan suatu kejadian peristiwa yang terjadi dalam suatu kerangka inersial, jika diamati oleh pengamat yang berada dalam kerangka acuan lain yang bergerak dengan kecepatan relatif konstan, digunakan transformasi Galileo. Perhatikan gambar berikut
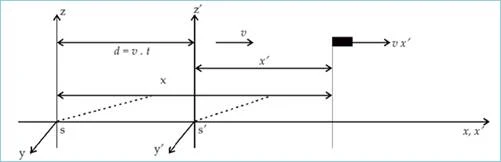 |
| Gambar 1. Transformasi Galileo |
Gambar 1 menggambarkan kerangka acuan S dengan sistem koordinat (x , y, z) dan kerangka acuan S’ dengan sistem koordinat (x’, y’, z’), di mana kerangka acuan S’ bergerak di dalam kerangka acuan S ke arah sumbu x positif dengan kecepatan relatif konstan sebesar v terhadap kerangka acuan S.
Misalkan kerangka acuan S adalah kerangka acuan yang digunakan oleh pengamat yang berada di stasiun dan kerangka acuan S’ digunakan oleh pengamat yang berada di dalam kereta api.
Mula-mula kedua kerangka acuan berimpit (t = 0), setelah bergerak selama t sekon maka kerangka acuan S’ telah menempuh jarak sejauh $d = v t$. Apabila bersamaan kereta itu bergerak, Asep juga berjalan di dalam gerbong kereta api, searah dengan gerak kereta dengan kecepatan $v’_x$ relatif terhadap kereta api, maka kedudukan Asep dapat dinyatakan dalam koordinat (x, y, z) terhadap kerangka S dan (x’, y, z’) terhadap kerangka S’. Sehingga kedudukan Asep antara kerangka acuan S’ terhadap S dapat dinyatakan :
$x’ = x – v.t, y’= y, z’= z, t’= t$
Persamaan ini dikenal dengan transformasi Gallileo
Kebalikan tranformasi Galileo dinyatakan :
$x = x’ + v.t’, y = y’,z = z’, t = t’$
Kecepatan Asep berjalan menurut pengamat yang berada di S dan S’ dapat ditentukan menurut transformasi Gallileo sebagai berikut :
Menurut pengamat di S’: Asep berjalan dengan kecepatan $v’_x$ sebesar
Menurut pengamat di S: Asep berjalan dengan kecepatan $v_x$ sebesar :
Dua persamaan ini merupakan penjumlahan kecepatan transformasi Galileo yang kemudian dikenal dengan penjumlahan kecepatan menurut teori Relativitas Newton.
Contoh 1. Ali naik kereta api yang bergerak dengan kecepatan 72 km/jam, di dalam kereta Ali berlari dengan kecepatan 2 m/detik. Tentukan kecepatan Ali menurut
a) Pengamat dalam kereta
b) Pengamat di stasion
Solusi:
Diketahui kecepatan kereta
a) kecepatan Ali menurut pengamat dalam kereta adalah$v’_{x}=2 m/s$
b) kecepatan Ali menurut pengamat di stasion adalah
Contoh 2. Seorang pengamat di bumi melihat sebuah pesawat luar angkasa bergerak dengan kecepatan 0,8c (dimana c adalah kecepatan cahaya yaitu $3⨉10^8$ m/s). sebuah elektron di dalam pesawat bergerak dengan kecepatan 0,9c. Tentukan kecepatan elektron diukur menurut pengamat di bumi
Solusi:
kecepatan elektron menurut pengamat di bumi adalah
Dalam kenyataannya, tak ada kecepatan benda yang melebihi kecepatan cahaya sehingga jawaban di atas tidak benar.
Oleh karena itu pada tahun 1905 Albert Einstein mengusulkan teori relativitas khusus. Teori ini bertolak pada kerangka acuan inersial yaitu kerangka acuan yang bergerak relatif dengan kecepatan konstan terhadap kerangka acuan yang lain.
Dalam mengemukakan teori relativitas khusus ini Einstein mengemukakan dua postulat dimana postulat keduanya membatasi kecepatan tertinggi sebagai kecepatan cahaya.
Teori relativitas Newton cocok untuk menjelaskan gerak-gerak benda jauh di bawah kecepatan cahaya dan tidak boleh digunakan untuk gerak-gerak benda mendekati kecepatan cahaya. Sedangkan teori relativitas Einstein berlaku untuk kecepatan rendah maupun mendekati kecepatan cahaya.

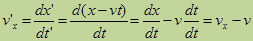
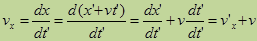

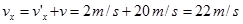
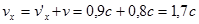









Tidak ada komentar:
Posting Komentar