Pada percobaan melempar dadu berisi enam mata secara berulang-ulang, frekuensi relatif munculnya mata dadu 1 kira-kira mendekati 1/6. Begitu pula mata dadu 2, mata dadu 3, mata dadu 4, mata dadu 5, dan mata dadu 6. Diklatakan bahwa munculnya salah satu dari keenam mata dadu itu mempunyai kesempatan yang sama.
Dengan menggunakan pemgertian kesempatan yang sama tersebut, suatu peluang klasik didefinisikan sebagai berikut.
Definisi 1:
Misalkan dalam suatu percobaan menyebabkan dapat munculnya salah satu dari n hasil yang mempunyai kesempatan yang sama (equally likely). Dan n kasil kejadian A muncul sebanyak k kali maka peluang kejadian A adalah
Contoh 1
Misalkan A adalah kejadian munculnya angka ganjil pada percobaan melempar sebuah dadu berisi enam. Berapa peluang kejadian A ?.
Jawab:
Banyak hasil yang mungkin muncul n = 6.
Kejadian muncul angka ganjil ada tiga yaitu 1, 3, dan 5. Maka k = 3.
Contoh 2
Suatu kotak berisi 4 bola putih dan 5 bola oranye. Dari kotak itu diambil satu bola secara acak.
a) Berapa peluang yang terambil itu bola putih?
b) Berapa peluang yang terambil itu bola oranye?
Jawab:
Total banyak bola adalah n = 4+5=9.
a) Banyak bola putih, k = 4.
b) Banyak bola oranye, k = 5.
Contoh 3
Suatu kotak berisi 9 bola. 4 bola putih dan 5 bola oranye. Dari kotak itu diambil 3 bola secara acak.
a) Berapa peluang yang terambil itu semuanya bola putih?
b) Berapa peluang yang terambil itu semuanya bola oranye?
c) Berapa peluang yang terambil itu 2 bola putih dan 1 bola oranye?
d) Berapa peluang yang terambil itu 1 bola putih dan 2 bola oranye?
Jawab:
Dari 9 diambil 3 bola, banyak cara mengambil ada
a) 3 bola putih dapat diambil dari 4 bola putih dengan banyak cara.
Peluang yang terambil itu semuanya bola putih adalah
b) 3 bola oranye dapat duambil dari 5 bola oranye dengan banyak cara
Peluang yang terambil itu semuanya bola oranye adalah
c) 2 bola putih dapat diambil dari 4 bola putih dengan banyak cara
1 bola oranye dapat diambil dari 5 bola oranye dengan banyak cara.
Berdasarkan kaidah perkalian, mengambil 2 bola putih dan 1 bola oranye dapat dilakukan dengan 6 x 5 = 30 cara. Maka
d) 1 bola putih dapat diambil dari 4 bola putih dengan banyak cara
2 bola oranye dapat diambil dari 5 bola oranye dengan banyak cara
Berdasarkan kaidah perkalian, mengambil 2 bola putih dan 1 bola oranye dapat dilakukan dengan 4 x 10 = 40 cara. Maka
Definisi peluang klasik dapat pula ditetapkan dengan pengertian ruang contoh
Definisi 2:
Misalkan S adalah ruang contoh dari suatu percobaan dengan setiap anggota S memiliki kesempatan yang sama.
Jika A adalah suatu kejadian dengan A⊂S (A hinpunan bagian dari S) maka peluang kedian A adalah
n(A) = banyak anggota dalam himpunan kejadian A.
n(S) = banyak anggota dalam hinpunan ruang contoh S.
Contoh 4
Misalkan A adalah kejadian munculnya angka genap pada percobaan melempar sebuah dadu berisi enam mata. Berapa peluang kejadian A ?.
Jawab:
Ruang contoh S={1,2,3,4,5,6}⟹n(S)=6.
Kejadian A={2,4,6}⟹n(A)=3.

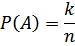
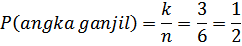
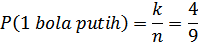
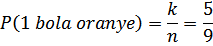
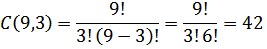
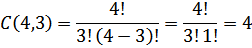
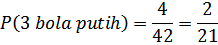
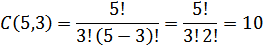
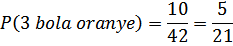
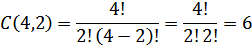
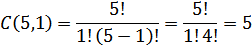
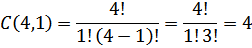
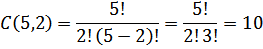
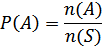
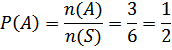









Tidak ada komentar:
Posting Komentar