1. Percobaan Michelson dan Morley
Pada mulanya sesuai dengan teori gelombang dari Huygens bahwa gelombang memerlukan medium rambatan untuk mencapai suatu tempat dan setelah Maxwell menyatakan bahwa cahaya tidak lain adalah gelombang elektromagnetik, maka para pakar fisika abad ke-19 segera melakukan berbagai usaha untuk mempelajari sifat zat perantara sebagai rambatan gelombang elektromagnetik. Para pakar mengajukan hipotesis medium yang dinamakan eter yang terdapat meskipun di ruang hampa . Pada tahun 1887, Michelsone dan Morley dua orang ilmuwan Fisika berkebangsaan Amerika mengukur kelajuan eter dengan menggunakan interferometer. Hakekat percobaan ini membandingkan kelajuan cahaya sejajar dan tegak lurus pada gerak bumi mengelilingi matahari. Andaikan eter itu diam di alam semesta ini diharapkan ada kelajuan relatif eter terhadap bumi yang bergerak mengelilingi matahari. Percobaan ini berdasarkan prinsip penjumlah vektor, dengan menggunakan penalaran gerak perahu yang menyeberangi sungai sebagai berikut.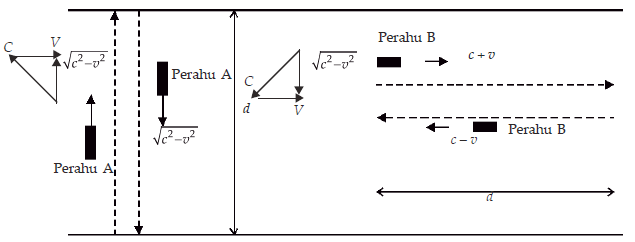 |
| Gambar 1. Gerak perahu menyeberangi sungai, perahu A bergerak tegak lurus arus sungai dan perahu B sejajar dengan arus sungai |
Perahu A bergerak menyeberangi sungai dalam lintasan tegak lurus sungai dan perahu B bergerak dengan lintasan sejajar arus sungai. Dengan membandingkan waktu yang diperlukan untuk menempuh jarak pulang pergi dalam lintasan tegak lurus arus sungai dan waktu yang diperlukan untuk menempuh lintasan yang sejajar arus sungai dalam jarak yang sama yaitu d seperti pada Gambar 1. Jika kecepatan perahu itu c, dan kecepatan aliran sungai adalah v. Kecepatan sesungguhnya perahu A menempuh lintasan adalah:
Untuk perahu B, kecepatan perahu sesungguhnya saat mengikuti arus adalah c + v dan saat menentang arus adalah c – v, sehingga waktu yang diperlukan untuk menempuh lintasan adalah :
Sehingga diperoleh perbandingan:
Apabila kecepatan perahu c diketahui dan dapat diukur, maka v dapat dihitung. Michelson dan Morley adalah perintis yang menggunakan contoh sederhana tersebut di atas untuk mencoba mengukur kecepatan aliran eter, bila memang eter itu ada. Perahu A dan perahu B diganti dengan pasangan berkas cahaya yang berasal dari satu sumber, yang satu dipantulkan dan yang lain diteruskan oleh gelas setengah cermin seperti tampak pada Gambar 2. Masing-masing berkas cahaya itu dipantulkan oleh cermin C1 dan C2 yang letaknya terhadap gelas setengah cermin. Berkas-berkas cahaya ini menggantikan peran perahu A dan B.
 |
| Gambar 2. Percobaan interferometer Michelson-Morley |
Apabila kecepatan cahaya itu sebesar $3 × 10^{8}$ m/s dan kecepatan eter relatif terhadap bumi sama dengan kecepatan tangensial bumi mengelilingi matahari yaitu sebesar $3 × 10^{4}$ m/s maka diharapkan ada selisih waktu antara $t_A$ dan $t_B$. Adanya selisih waktu itu diharapkan antara gelombang cahaya yang berasal dari pantulan cermin C1 dan C2 akan timbul perubahan polapola hasil interferensi yang terjadi pada layar pengamatan. Akan tetapi selama percobaan tidak pernah teramati adanya perubahan pola-pola interferensi yang terjadi. Hal ini menunjukkan bahwa tidak ada perbedaan waktu antara $t_A$ dan $t_B$.. Berdasarkan percobaan ini Michelson dan Morley menyimpulkan bahwa : - Hipotesa tentang eter itu tidak benar, eter itu tidak ada. - Kecepatan cahaya adalah sama untuk ke segala arah, tidak tergantung pada kerangka acuan inersial.
2 Relativitas (khusus) Einstein dan Transformasi Lorentz
Percobaan Michelson dan Morley telah membuktikan secara tidak langsung bahwa eter itu tidak ada. Pada tahun 1905 Albert Einstein mengusulkan teori relativitas khusus. Teori ini bertolak pada kerangka acuan inersial yaitu kerangka acuan yang bergerak relatif dengan kecepatan konstan terhadap kerangka acuan yang lain. Sepuluh tahun kemudian pada tahun 1915, Einstein mengemukakan teori relativitas umum yang bertolak dari kerangka acuan yang bergerak dipercepat terhadap kerangka acuan yang lainnya. Pada postingan ini kita hanya akan mempelajari teori relativitas khusus saja.Dalam mengemukakan teori relativitas khusus ini Einstein mengemukakan dua postulat yaitu :
1. Hukum Fisika dapat dinyatakan dalam bentuk persamaan yang berbentuk sama pada semua kerangka acuan inersial.
2. Kecepatan cahaya di dalam ruang hampa ke segala arah adalah sama untuk semua pengamat dan tidak tergantung pada gerak sumber cahaya atau pengamat.
Pada postulat yang pertama tersebut menyatakan ketiadaan kerangka acuan universal. Apabila hukum fisika berbeda untuk pengamat yang berbeda dalam keadaan gerak relatif, maka kita dapat menentukan mana yang dalam keadaan “diam” dan mana yang “bergerak” dari perbedaan tersebut. Akan tetapi karena tidak ada kerangka acuan universal, perbedaan itu tidak terdapat, sehingga muncullah postulat ini. Postulat pertama menekankan bahwa prinsip Relativitas Newton berlaku untuk semua rumus Fisika, tidak hanya dalam bidang mekanika, tetapi pada hukum-hukum Fisika lainnya. Sedangkan postulat yang kedua sebagai konsekuensi dari postulat yang pertama, sehingga kelihatannya postulat kedua ini bertentangan dengan teori Relativitas Newton dan transformasi Galileo tidak berlaku untuk cahaya. Dalam postulat ini Einstein menyatakan bahwa selang waktu pengamatan antara pengamat yang diam dengan pengamat yang bergerak relatif terhadap kejadian yang diamati tidak sama (t ≠t’). Menurut Einstein besaran kecepatan, waktu, massa, panjang adalah bersifat relatif. Untuk dapat memasukkan konsep relativitas Einstein diperlukan transformasi lain, yaitu transformasi Lorentz.
Transformasi Lorentz
Pada transformasi Galileo telah dikemukakan bahwa selang waktu pengamatan terhadap suatu peristiwa yang diamati oleh pengamat yang diam dengan pengamat yang relatif bergerak terhadap peristiwa adalah sama. Hal inilah yang menurut Einstein tidak benar, selang waktu pengamatan antara pengamat yang diam dan pengamat yang bergerak relatif adalah tidak sama. Transformasi Lorentz pertama kali dikemukaan oleh Hendrik Anton Lorentz, seorang fisikawan dari Belanda pada tahun 1895. Karena waktu pengamatan oleh pengamat yang diam pada kerangka acuan S dan pengamat yang bergerak pada kerangka acuan S’ hubungan transformasi Galileo haruslah mengandung suatu tetapan pengali yang disebut tetapan transformasi. Sehingga persamaan yang menyatakan hubungan antara koordinat pada kerangka acuan S dan S’ dituliskan sebagai berikut :Kebalikan transformasi Lorentz
di mana γ(gamma) adalah tetapan transformasi yang tergantung pada kecepatan benda.
Faktor γ pada kedua persamaan di atas adalah sama, karena tidak ada perbedaan antara kerangka S dan S’ dan tidak ada perbedaan antara koordinat y,y’ dan z,z’. Hal ini dikarenakan kerangka acuan S’ bergerak ke arah sumbu x positif pada kerangka S dengan kecepatan tetap sebesar v, yang berbeda adalah t dan t’, perbedaan ini dapat kita lihat jika kita mensubstitusikan persamaan $x=γ(x’+vt’)$ ke dalam perasamaan x’, atau $x’=γ(x-vt)$ ke dalam perasamaan x sbb:
| mendapatkan t | mendapatkan t' |
|
|
|
Misalkan kecepatan cahaya pada kerangka acuan S’ adalah $v_{x’}= c$, maka menurut postulat Einstein yang kedua menyatakan bahwa pengamat pada kerangka acuan S akan mendapatkan $v_{x} = c$, maka didapatkan bahwa : x = c.t .... (1) dan x’= c.t’…(2) Bila nilai x dan t dimasukkan pada persamaan (1) atau x’ dan t’ dimasukkan pada persamaan (2) kita bisa dapatkan nilai γ sbb:
| cara 1 | cara 2 |
|
|
|
Sehingga transformasi Lorentz dituliskan menjadi :
Kebalikan transformasi Lorentz dapat dituliskan menjadi :
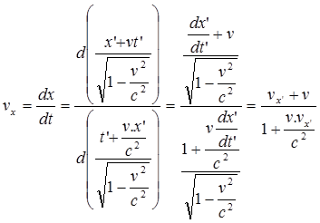
Maka transformasi Lorentz untuk kecepatan benda yang bergerak dapat dinyatakan :
Secara analog persamaan transformasi Lorentz balik untuk kecepatan dapat dituliskan :
Persamaan-persamaan tersebut di atas merupakan rumus kecepatan benda yang diamati oleh pengamat yang diam yang disebut rumus penambahan kecepatan relativistik yang sesuai dengan teori relativitas Einstein. Sekarang mari kita uji dengan menggunakan kejadiankejadian yang kita alami dalam kehidupan kita.
a. Bila $v_{x’}= 0$ maka $v_{x} = v$ ini cocok dengan kejadian dalam kehidupan kita, jika penumpang kereta api diam kecepatan penumpang terhadap tanah sama dengan kecepatan kereta api terhadap tanah.
b. Bila $v = 0$ maka $v_{x} = v_{x’}$ hal ini juga sesuai yang kita harapkan, yaitu jika kereta api diam, maka kecepatan penumpang terhadap tanah sama dengan kecepatan penumpang terhadap kereta api.
c. Bila $v$ dan $v_{x’}$ sangat kecil dibandingkan kecepatan cahaya maka $v_{x} = v_{x’}+ v$ hal ini sesuai dengan rumus kecepatan dalam transformasi Galileo.
d. Bila $v_{x’}= c$ dan $v = c$ maka diperoleh nilai $v_{x} = c$, hal ini sesuai dengan postulat Einstein yang kedua.
Ternyata rumus pertambahan kecepatan relativistik yang diturunkan dari transformasi Lorentz tidak bertentangan dengan kecepatan relativistik.
Contoh 1 Sebuah pesawat tempur yang bergerak dengan kecepatan 0,8 c relatif terhadap bumi menembakkan roket dengan kecepatan 0,6 c. Berapakah kecepatan roket tersebut menurut pengamat yang diam di bumi?
Penyelesaian : Diketahui : $v = 0,8 c, v_{x’}= 0,6 c$ Ditanyakan : $v_{x} = ?$
Contoh 2 Sebuah wahana antariksa bergerak melewati bumi dengan kecepatan 0,8 c relatif terhadap bumi, sebuah pesawat antariksa meluncur dari wahana tersebut dengan kecepatan 0,6 c. Berapakah kecepatan bumi menurut pengamat yang diam di pesawat antariksa?
Penyelesaian : Diketahui : $v = 0,8 c, v_{x}= -0,6 c$ (tanda negatif karena bumi menjauhi pengamat )
Ditanyakan : $v_{x’} = ?$

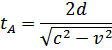
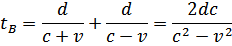


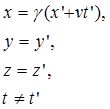
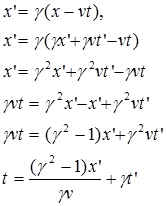
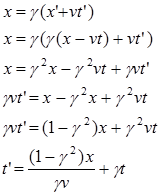

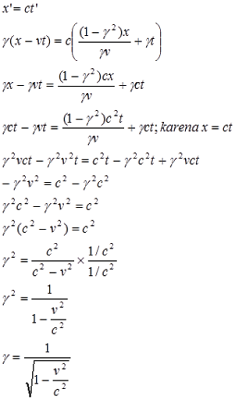
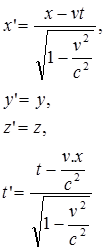
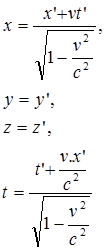
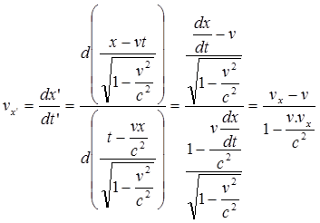

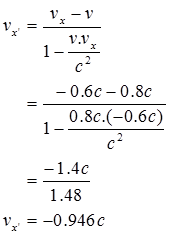









ليست هناك تعليقات:
إرسال تعليق