1 Distribusi HiperGeometrik
Misalkan ada sebuah populasi berukuran $N$, diantaranya termasuk $D$ buah termasuk kategori tertentu. Dari populasi itu diambil sample acak berukuran $n$. berapakah dalam sampel yang terambil itu akan ada $x$ buah kategori $D$ ?. jawabannya dapat ditentukan dengan distribusi Hipergeometrik yaitu:Dengan $ x = 0, 1, 2, …, n$.
Rumus distribusi peluang ini merupakan rumus dengan variabel acak diskrit. Disini jelah berlaku Σp(x) = 1 dengan penjumlahan dilakukan untuk semua harga $x = 0, 1, 2, …, n$.
Contoh 1. Sekelompok manusia terdiri dari 20 orang dan 7 diantaranya lahir pada tanggal 1 Januari. Secara acak akan diambil 5 orang. Berapa peluang diantara yang 5 orang tersebut.
a) Tidak terdapat yang lahir pada tanggal 1 Januari
b) Terdapat tidak lebih 1 orang yang lahir pada tanggal 1 Januari
c) Terdapat 4 orang yang lahir pada tanggal 1 Januari
d) semuanya lahir pada tanggal 1 Januari
Solusi:
Diketahui $N=20, D=7, n=5$.
a) Peluang tidak terdapat yang lahir pada tanggal 1 Januari maka $x=0$.
b) Terdapat tidak lebih 1 orang yang lahir pada tanggal 1 Januari maka $x=1$
c) Terdapat 4 orang yang lahir pada tanggal 1 Januari maka $x=4$
d) semuanya lahir pada tanggal 1 Januari maka $x=5$
2 Distribusi Poisson
Distribusi Poisson sering digunakan untuk menentukan atau menghitung peluang sebuah peristiwa yang dalam kesempatan tertentu harapan terjadinya sangat jarang. Sebuah variabel acak diskrit $X$ dikatakan mempunyai distribusi poisson jika fungsi peluangnya berbentukDengan $ x = 0, 1, 2, …, n$, $e=2,7183$, dan λ (lamda) sebuah konstanta. Distribusi poisson mempunyai parameter yaitu
Contoh 2. Misalkan terdapat rata-rata 1,4 orang buta huruf untuk 100 orang. Sebuah sampel berukuran 200 telah diambil.
a) Berapa peluang tidak terdapat buta huruf ?
b) Berapa peluang terdapat 1 orang buta huruf?
c) Berapa peluang terdapat 10 orang buta huruf?
Solusi: Diketahui
a) peluang tidak terdapat buta huruf berarti $x=0$
b) peluang terdapat 1 orang buta huruf berarti $x=1$
c) peluang terdapat 10 orang buta huruf berarti $x=10$

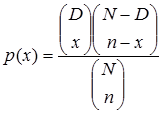




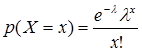
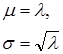

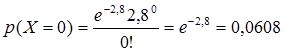
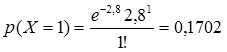
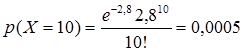










ليست هناك تعليقات:
إرسال تعليق