Transpose Matriks
Transpose
suatu matriks A ditulis dengan notasi AT (dibaca “A transpos” dan
tidak dibaca “A pangka T”) atau At. Kata “transpose” adalah gabungan
dua kata, “trans” yang berarti perpindahan dan “pose” yang berarti letak. Jadi transpose
dapat diartikan sebagai perpindahan letak.
Definisi:
Misalkan A adalah matriks berordo m×n,
transpose A diperoleh dengan memindahkan
elemen-elemen pada baris-baris matriks A ke dalam kolom-kolom pada matriks baru
yang berordo n×m secara berurutan.
Yang
dimaksud berurutan di sini adalah: elemen-elemen pada baris pertama matriks A dipindahkan
ke dalam kolom pertama matriks baru, elemen-elemen pada baris kedua matriks A dipindahkan
ke dalam kolom kedua matriks baru, dan seterusnya.
Contoh
1
Dalam
kasus matriks persegi, ordo matriks sebelum dan sesudah ditransposkan sama(mxn=nxm).
Dalam hal ini kita memerlukan notasi berbeda untuk matriks yang baru agar tidak
terjadi kesalahan
.
Contoh
2
Perhatikan,
jika notasi matriks baru tidak dibedakan maka akan menghasilkan kesimpulan seperti
ini
Padahal
jelas kesimpulan ini salah karena melanggar definisi kesamaan matriks. Dan yang
benar adalah
Namun
kesalahan dapat dihindari jika penulisan notasi dibatasi sampai notasi matriks
transpose saja baik dengan menyertakan ordo matriks maupun tidak.
Contoh
3
Kesamaan Matriks
Pada
contoh 2 telah disinggung mengenai kesamaan matriks. Untuk lebih jelasnya
perhatikan definisi berikut
Definisi:
Dua
matriks dikatakan sama apabila ordo kedua matriks sama dan elemen-elemen yang
seletak dari kedua matriks juga sama.
Contoh
4. Diketahui
Maka
A ≠ B, meskipun ordonya sama, karena satu elemen yang
seletak tidak sama yaitu 10 ≠ 12.
A = C, karena ordonya sama dan elemen-elemen yang
seletak juga sama, kususnya 10 = 20/2 dan 7 = 21/3.
A ≠ D, karena ordonya beda.
Contoh
5. Tentukan nilai a dan b dari kesamaan matriks berikut
Jawab:
Baca juga: soal-dan-pembahasan-matriks

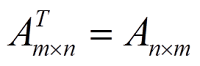
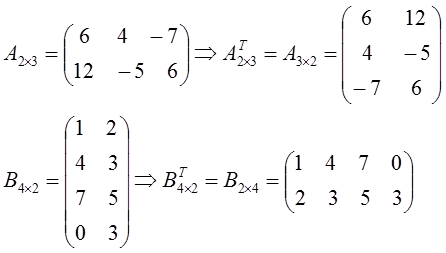
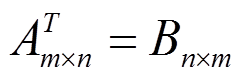
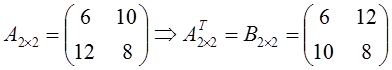
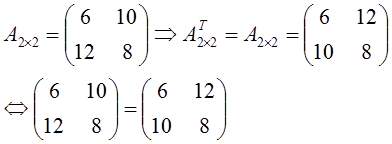
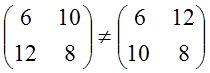
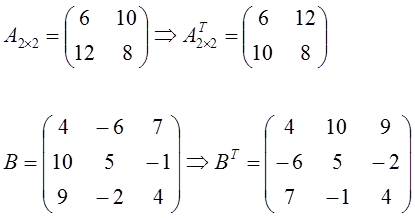
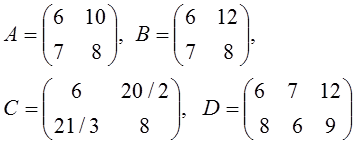
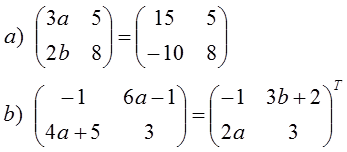
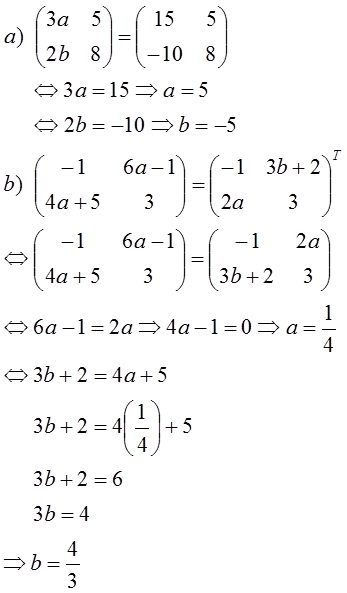









Tidak ada komentar:
Posting Komentar