Agar langkah-langkah penyelesaian SPLDV dengan metode substitusi atau pertukaran variabel mudah dipahami, mari perhatikan SPLDV berikut
Untuk menyelesaikan SPLDV dengan metode substitusi ditempuh langkah-langkah sbb:
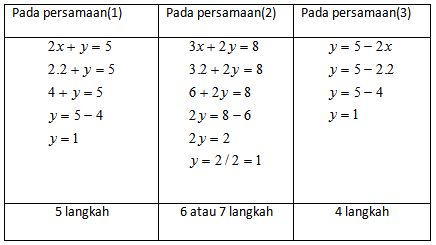
Langkah 1. Pilih persamaan yang mempunyai nilai mutlak koefisien/pengali terkecil, jika ada. Jika ada beberapa koefisien terkecil yang sama, pilih yang mana saja. Pada spldv diatas, variabel yang koefisiennya paling kecil adalah y pada persamaan 1. Jadi kita pilih persamaan
Langkah 2. Ubah persamaan terpilih menjadi bentuk persamaan explisit. Variabel dengan koefisien terkecil sebagai variabel terikat. Namai persamaan ini sebagai persamaan(3) atau persamaan sementara.
Langkah 3. Masukan persamaan(3) pada persamaan yang bukan asalnya, berarti ke persamaan(2).
Maka didapat nilai x = 2.
Bagaimana jika persamaan(3) dimasukan ke persamaan asalnya ?. Jika dimasukan ke persamaan asalnya, maka akan didapatkan kebenaran namun tidak akan didapatkan nilai variabel manapun. Perhatikan !.
tidak ada nilai variabel yang didapatkan.
Langkah 4. Masukan nilai variabel yang didapat dari langkah 3 ke persamaan mana saja, hasilnya sama. Namun akan lebih cepat jika dimasukan ke persamaan(3). Perhatikan !.
Langkah 5. Tuliskan himpunan penyelesaian (HP) dalam bentuk HP={(nilai x, nilai y)}.
Jadi, himpunan penyelesaian SPLDV di atas adalah HP={(2,1)}.
Jawab :
Kita pilih persamaan(2), ubah x sebagai variabel terikat ( dan y sebagai variabel bebas). Didapat
Masukkan persamaan(3) ke persamaan(1), didapat
Masukkan y =7 ke persamaan(3),didapat
Jadi, HP = { (-6, 9)}.
Untuk contoh lainnya silakan tonton di https://www.youtube.com/watch?v=FJNLA8RZyUg
Untuk menyelesaikan SPLDV dengan metode substitusi ditempuh langkah-langkah sbb:
Langkah 1. Pilih persamaan yang mempunyai nilai mutlak koefisien/pengali terkecil, jika ada. Jika ada beberapa koefisien terkecil yang sama, pilih yang mana saja. Pada spldv diatas, variabel yang koefisiennya paling kecil adalah y pada persamaan 1. Jadi kita pilih persamaan
Langkah 2. Ubah persamaan terpilih menjadi bentuk persamaan explisit. Variabel dengan koefisien terkecil sebagai variabel terikat. Namai persamaan ini sebagai persamaan(3) atau persamaan sementara.
Langkah 3. Masukan persamaan(3) pada persamaan yang bukan asalnya, berarti ke persamaan(2).
Maka didapat nilai x = 2.
Bagaimana jika persamaan(3) dimasukan ke persamaan asalnya ?. Jika dimasukan ke persamaan asalnya, maka akan didapatkan kebenaran namun tidak akan didapatkan nilai variabel manapun. Perhatikan !.
tidak ada nilai variabel yang didapatkan.
Langkah 4. Masukan nilai variabel yang didapat dari langkah 3 ke persamaan mana saja, hasilnya sama. Namun akan lebih cepat jika dimasukan ke persamaan(3). Perhatikan !.
Langkah 5. Tuliskan himpunan penyelesaian (HP) dalam bentuk HP={(nilai x, nilai y)}.
Jadi, himpunan penyelesaian SPLDV di atas adalah HP={(2,1)}.
Contoh.
Tentukan himpunan penyelesaian SPLDVJawab :
Kita pilih persamaan(2), ubah x sebagai variabel terikat ( dan y sebagai variabel bebas). Didapat
Masukkan persamaan(3) ke persamaan(1), didapat
Masukkan y =7 ke persamaan(3),didapat
Jadi, HP = { (-6, 9)}.
Untuk contoh lainnya silakan tonton di https://www.youtube.com/watch?v=FJNLA8RZyUg

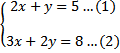
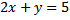
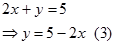
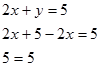
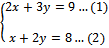
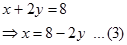
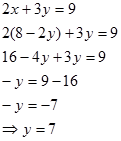
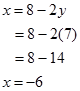









Tidak ada komentar:
Posting Komentar