Barisan Aritmatika
Suatu barisan $u_1, u_2, …, u_n$ disebut barisan aritmatika jika mempunyai nilai beda yang tetap antara satu suku dengan satu suku berikutnya, yaitu
$u_{n}-u_{n-1}=b$
dengan $b$ bilangan tetap yang disebut beda, yang tidak tergantung pada $n$
Barisan ini mempunyai rumus suku ke-n:


dimana
$u_n$ : suku ke n
$n = 1,2,3, …$
$a$ : suku awal
$b$ : beda
Contoh 1 . carilah suku pertama, beda dan suku ke-6 pada dua barisan berikut
a) $5, 14, 23, …$
b) $4, 0, -4, -8, …$
Jawab:
a) Suku pertama $a = 5$, beda $b = 14-5=9$
Suku ke-6

a) Suku pertama $a = 5$, beda $b = 14-5=9$
Suku ke-6

b) Suku pertama $a = 4$, beda $b = 0-4=-4$
Suku ke-6

Contoh 2. Suku kedua barisan aritmatika adalah 12, sedangkan suku ke-11 adalah 39.
a) Carilah suku pertama dan bedanya
b) Tentukanlah rumus suku ke-n nya
Jawab:


a) Kurangi persamaan (1) oleh persamaan (2), didapat $b=3$.
Tukarkan $b=3$ ke persamaan (1) atau (2), didapat $a=9$.
Jadi, suku pertamanya 9 dan bedanya 3
b) rumus suku ke-n


Contoh 3(penerapan). Sebuah keluarga besar mempunyai 15 orang anak. Anak bungsunya berumur 10 tahun dan anak ke-10 nya berumur 20 tahun.
a) Berapakah umur anak pertamanya?.
b)Tuliskan barisan umur anak-anak kelurga tersebut
Kurangi persamaan (1) oleh persamaan (2), didapat $b=-2$.
Tukarkan $b=-2$ ke persamaan (1) atau (2), didapat $a=38$.
Jadi, anak pertamanya berumur 38 tahun.
b) $38,36,34,32,30,28,26,24,22,20,18,16,14,12,10 $
Suku tengah
Perhatikan barisan-barisan aritmatika berikut. Banyak suku pada tiap barisan ini ganjil.
a) $u_1, u_2, u_3$; banyak suku 3 dan suku tengahnya $u_2$.
Suku tengah $u_2$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_2=a+b=\frac{1}{2}(2a+2b) =\frac{1}{2}(a+(a+2b))=\frac{1}{2}(u_1+u_3)$
b) $u_1, u_2, u_3, u_4, u_5$; banyak suku 5 dan suku tengahnya $u_3$.
Suku tengah $u_3$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_3=a+2b=\frac{1}{2}(2a+4b) =\frac{1}{2}(a+(a+4b))=\frac{1}{2}(u_1+u_5)$
c) $u_1, u_2, u_3, u_4, u_5, u_6, u_7$; banyak suku 7 dan suku tengahnya $u_4$.
Suku tengah $u_4$ dapat dirumuskan dengan bantuan manipulasi aljabar sbb:
$u_4=a+3b=\frac{1}{2}(2a+6b) =\frac{1}{2}(a+(a+6b))=\frac{1}{2}(u_1+u_7)$
Secara umum untuk barisan aritmatika $u_1, … , u_k, … , u_{2k-1}$; banyak suku $2k-1, k>=2, k$ bilangan asli,
suku tengahnya $u_k$ dapat dirumuskan sbb:
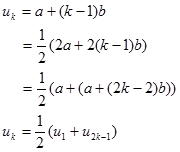
Contoh 4. Diketahui barisan $3, 6, 9, …,153$. Banyak suku barusan itu ganjil. a)Cari suku tengahnya
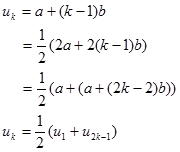
Contoh 4. Diketahui barisan $3, 6, 9, …,153$. Banyak suku barusan itu ganjil. a)Cari suku tengahnya
b)Suku ke berapakah itu ?
c)Berapa banyak suku barisan itu ?
Jawab:
Diketahui $a = 3, b=3$, suku terakhir $ u_{2k-1}=153$
Diketahui $a = 3, b=3$, suku terakhir $ u_{2k-1}=153$
a)$u_k=\frac{1}{2}(u_1+u_{2k-1})=\frac{1}{2}(3+153)=\frac{156}{2}=78$
b) $u_k=a+b(k-1)=78$
$3+3(k-1)=78$
$3k=78$
$k=\frac{78}{3}=26$
c) Banyak suku barisan itu $2k-1=2.26-1=52-1=51$ suku
Sisipan
Misalkan di antara dua bilangan ril $a$ dan $c$ ($a\neq c$) disisipkan sebanyak $k$ buah bilangan ($k$ bilangan asli), sehingga bilangan-bilangan campuran membentuk barisan aritmatika. Pertanyaannya adalah berapakah beda barisan aritmatika yang terbentuk itu ?. untuk menjawab pertanyaan itu, kita misalkan bedanya $b$. Dengan pemisalan itu, barisan aritmatika yang terbentuk dapat dinyatakan sbb:
Untuk menentukan bedanya, kurangkan suku terakhir oleh suku sebelummya




Contoh 5. Diantara bilangan 3 dan 30 disisipkan enam bilangan sehingga bilangan-bilangan campuran membentuk barisan aritmatika. Cari beda barisan itu
Jawab:
Diketahui $a=3, c=30$ dan $k =6$

Diketahui $a=3, c=30$ dan $k =6$

Deret aritmatika
Jika barisan $u_1, u_2, …, u_n$ adalah barisan aritmatika maka $u_1 + u_2 +…+u_n$ adalah deret aritmatika.
Jumlah $n$ suku pertama barisan aritmatika adalah
$S_n = u_1 + u_2 +u…+ u_n$
Untuk mempermudah mendapatkan hasil $S_n$ dipakai metode berikut
Selanjutnya gantikan $u_{n-1}$ oleh $u_n -b$ dan $u_{n-2}$ oleh $u_n -2b$
$S_n=a+(a+b)+(a+2b)+...+u_{n-2}+u_{n-1}+u_n$ ............(1)
Jika urutan penjumlahan pada (1) dibalik maka
$S_n=u_n+u_{n-1}+u_{n-2}+...+(a+2b)+(a+b)+a$ ............(2)
Dengan menjumlahkan (1) dan (2) didapat
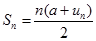
Contoh 6. Tentukan jumlah 1000 suku pertama deret bilangan ganjil
Selanjutnya gantikan $u_{n-1}$ oleh $u_n -b$ dan $u_{n-2}$ oleh $u_n -2b$
$S_n=a+(a+b)+(a+2b)+...+u_{n-2}+u_{n-1}+u_n$ ............(1)
$S_n=u_n+u_{n-1}+u_{n-2}+...+(a+2b)+(a+b)+a$ ............(2)
Dengan menjumlahkan (1) dan (2) didapat
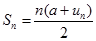
Bentuk lainnya didapat dengan mengganti $u_n$ dengan suku deret aritmatika
Contoh 6. Tentukan jumlah 1000 suku pertama deret bilangan ganjil
a) Memakai
suku ke-n tanpa beda
b) Memakai
beda tanpa suku ke-n
Jawab:
Deret bilangan ganjil adalah $1+3+5+…+2n-1$.
$u_n = 2n-1, a=1, b=2$ dan $n=1000$.
a) $S_{1000}=\frac{1000(1+2000-1)}{2}=500(2000)=1000000$
b) $S_{1000}=\frac{1000(2+(1000-1)(2)}{2}=500(2000)=1000000$














ليست هناك تعليقات:
إرسال تعليق