1 Distribusi Binom
Perhatikan eksperimen yang menghasilkan dua peristiwa A dan bukan A ditulis $\bar{A}$, dengan peluang terjadinya A adalah $P(A)=\pi$.Jika dalam percobaan dalam eksperimen itu peluang terjadinya A, $P(A)=\pi$ harganya tetap, maka percobaan yang berulang dalam eksperimen dinamakan percobaan Bernoulli. Jika percobaan Bernoulli dilakukan secara independen sebanyak $N$ kali, $X$ menghasilkan peristiwa $A$ dan $(N-X)$ menghasilkan peristiwa Ā $\bar{A}$. Jika $P(A)=\pi$ dan $P(\bar{A})=1-\pi$, maka peluang terjadinya $A$ sebanyak $X=x$ kali di antara $N$ dihitung dengan rumus
Rumus distribusi peluang ini merupakan rumus dengan variabel acak diskrit yang disebut distribusi binom.
Disini jelah berlaku $Σp(x) = 1$ dengan penjumlahan dilakukan untuk semua harga $x = 0, 1, 2, …, N$.
Distribusi binom ini mempunyai parameter- parameter yang ditinjau dari peristiwa A antara lain $μ$ (mu kecil) untuk rata-rata dan $σ$ (sigma kecil) untuk simpangan baku yang dirumuskan dengan:
Contoh 1. Cari peluang mendapatkan 7 kali sisi angka A ketika melakukan 10 kali lemparan dengan uang logam homogen (sama).
Solusi:
peluang mendapatkan sisi angka A dalam satu lemparan adalah π = ½, maka
Jadi, peluang mendapatkan 7 kali sisi angka A ketika melakukan 10 kali lemparan adalah 0,1172.
Contoh 2 . 10% lulusan tertentu tergolong pengangguran. Sebuah sampel berukuran 20 telah diambil secara acak dari lulusan tertentu . Berapa peluang itu akan berisi pengangguran?
a)1 orang
b) 5 orang
c)paling sedikit 2 orang
d) paling banyak 3 orang
e)semuanya
f)tentukan rata-rata terdapat pengangguran
solusi:
kita artikan $X $= lulusan tertentu . Maka $π $= peluang berisi pengangguran = 10% = 0,1.
a)peluang berisi 1 orang pengangguran
b) peluang berisi 5 orang pengangguran
c) peluang berisi paling sedikit 2 orang pengangguran
d) peluang berisi paling banyak 3 orang
e)semuanya berisi pengangguran
Sebuah harga yang sangat kecil setara dengan 0 (hampir tidak mungkin semuanya berisi pengangguran).
f)rata-rata terdapat pengangguran
Jadi, diharapkan didapat rata-rata terdapat 2 pengangguran.
2. Distribusi Multinom
Distribusi binom dapat diperluas untuk menghitung peluang beberapa peristiwa sekaligus dengan sifat setiap peristiwa menghasilkan dua peristiwa E dan bukan E. Hasil perluasan distribusi binom ini disebut distribusi multinom.Misalkan sebuah eksperimen menghasilkan peristiwa $E_{1}, E_{2},…, E_{k}$ dengan peluang-peluang $P(E_{1})=\pi_{1}, P(E_{2})=\pi_{2},,…, P(E_{k})=\pi_{k}$ dan $\pi_{1}+\pi_{2}+…+\pi_{k}=1$. Terhadap eksperimen ini dilakukan percobaan sebanyak $N$ kali. Maka peluang akan terdapat $x_1$ peristiwa $E_1$, $x_2$ peristiwa $E_2$,…,$x_k$ peristiwa $E_k$ diantara $N$ ditentukan oleh distribusi multinom dengan rumus
Dengan
Distribusi multinom ini mempunyai parameter- parameter yang ditinjau dari peristiwa $E_i$ yaitu $μ_i$ untuk rata-rata dan $σ_{i}^2$ untuk varians yang dirumuskan dengan:
Solusi:
Peluang dari mesin A, $\pi_{1}=P(A)=\frac{4}{22}, x_{1}=2$,
Peluang dari mesin B, $\pi_{2}=P(B)= \frac{5}{22}, x_{2}=3$,
Peluang dari mesin C, $\pi_{3}=P(C)= \frac{6}{22}, x_{3}=1$,
Peluang dari mesin D, $\pi_{4}=P(D)= \frac{7}{22}, x_{4}=4$.
Maka

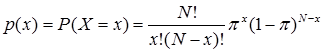
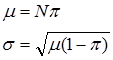
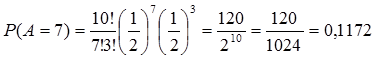
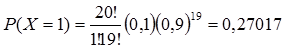
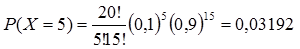
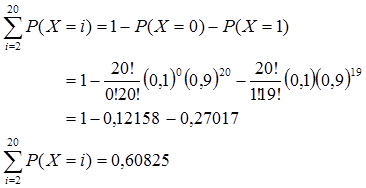
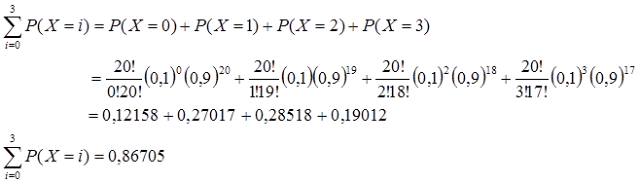
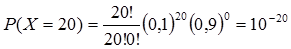
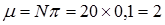
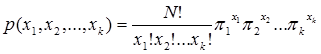
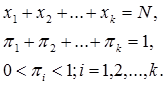

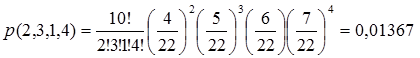










ليست هناك تعليقات:
إرسال تعليق