Jenis-jenis matriks dapat dikelompokkan berdasarkan elemen, ordo, dan elemen dan ordonya.
A. berdasarkan elemennya
1) Matriks Nol
Matriks nol adalah matriks yang seluruh elemennya nol.
Contoh
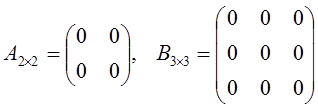
B. Berdasarkan ordonya
2 ) Matriks persegi
adalah matriks yang banyaknya barisnya sama dengan banyaknya kolomnya.
Jika banyak baris = banyak kolom = n , maka ordonya adalah n×n.
Contoh
Contoh
3)
matriks baris/vektor baris
adalah
matriks yang terdiri satu baris dan n kolom, n>=2. Ordonya adalah 1×n
Contoh
4)
matriks kolom/vektor kolom
adalah
matriks yang terdiri m baris, m>=2 dan satu kolom. Ordonya adalah m×1
Contoh
5)
matriks datar/ horizontal
adalah
matriks yang banyak baris m kurang dari banyak kolom n.
Contoh
adalah
matriks yang banyak baris m lebih banyak dari banyak kolom n.
C. Berdasarkan elemen dan ordonya
7) Matriks diagonal
adalah matriks persegi yang elemen-elemem di atas dan di bawah diagonal utamanya nol.
Contoh
8) Matriks tridiagonal
adalah matriks persegi
yang elemen-elemem di atas dan di bawah diagonal utamanya nol kecuali
pada sisi kanan dan kirinya.
Contoh
9) Matriks skalar
adalah matriks diagonal
yang semua elemen pada diagonal utamanya sama.
Contoh
adalah matriks persegi yang setiap elemennya, selain elemen diagonal
utama, adalah simetris terhadap diagonal utama.
11) Matriks simetri miring
adalah matriks simetri yang elemen-elemennya, selain elemen diagonal
utama, saling berlawanan.
12) Matriks Segitiga
Atas
adalah matriks persegi yang
elemen-elemen di bawah diagonal utama seluruhnya nol. Jika
elemen-elemen pada diagonal utama, baris pertama dan kolom terakhir dihubungkan
dengan garis lurus maka akan berbentuk segitiga siku-siku di atas elemen-elemen
nol, dari sinilah istilah Matriks Segitiga Atas tersebut.
Contoh
13) Matriks Segitiga
Bawah
adalah matriks persegi yang
elemen-elemen di atas diagonal utama seluruhnya nol. Jika
elemen-elemen pada diagonal utama, kolom pertama dan baris terakhir dihubungkan
dengan garis lurus maka akan berbentuk segitiga siku-siku di bawah
elemen-elemen nol, dari sinilah istilah Matriks Segitiga bawah tersebut.
Contoh
14) Matriks Identitas/ satuan
Adalah matriks diagonal
yang semua elemen pada diagonal utamanya 1. Matriks Identitas diberi lambang I (
huruf i besar) dan berperan penting dalam konsep matriks. Matriks ini analog dengan
bilangan 1 yang menjadi identitas perkalian pada bilangan real.
Contoh
Matriks identitas mempunyai
sifat:
Jika A
dan I
berordo sama, maka untuk setiap matrik persegi A
berlaku AI=IA=A.

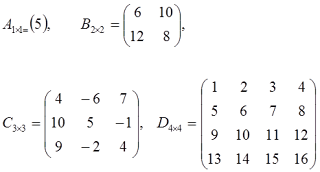
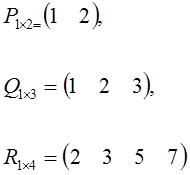
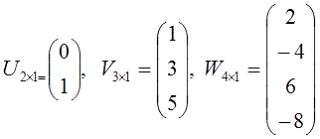
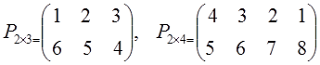
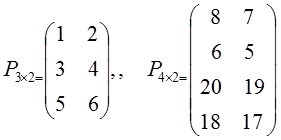
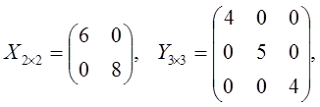
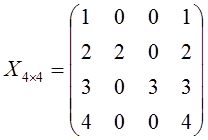
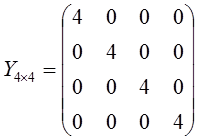
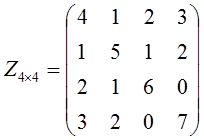
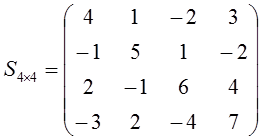
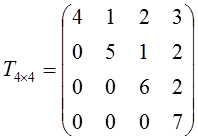
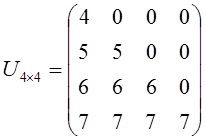
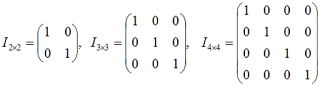







ليست هناك تعليقات:
إرسال تعليق